A charge of −3.00μC is fixed at the center of a compass. Two additional charges are fixed on the circle of the compass (radius 0.100 m). The charges on the circle are −4.00μC at the position due north and +5.00μC at the position due east. what is the magnitude and direction of the net electrostatic force acting on the charge at the center ? Specify the direction relative to due east.
3.60N,51.3∘ north of east
34.6N,36.3∘ north of east
14.4N,44.2∘ north of east
17.3N,38.7∘ south of east
The correct Answer is:D
To solve the problem, we need to calculate the net electrostatic force acting on the charge at the center due to the two charges fixed on the circle.
1. Identify the Charges and Their Positions:
- Charge at the center (Q1): −3.00μC=−3.00×10−6C
- Charge due North (Q2): −4.00μC=−4.00×10−6C
- Charge due East (Q3): +5.00μC=+5.00×10−6C
- Radius of the compass (r): 0.100m
2. Calculate the Forces Due to Each Charge:
- Force due to Q2 (F1):
F1=k|Q1⋅Q2|r2
Where k=8.99×109N⋅m2/C2.
F1=8.99×109|−3.00×10−6⋅−4.00×10−6|(0.100)2
F1=8.99×10912.00×10−120.01=8.99×109⋅1.2×10−9=10.788N
This force acts towards the south (since both charges are negative).
- Force due to Q3 (F2):
F2=k|Q1⋅Q3|r2
F2=8.99×109|−3.00×10−6⋅5.00×10−6|(0.100)2
F2=8.99×10915.00×10−120.01=8.99×109⋅1.5×10−9=13.485N
This force acts towards the east (since the center charge is negative and the east charge is positive).
3. Determine the Net Force:
- The forces F1 and F2 are perpendicular to each other (south and east).
- We can use the Pythagorean theorem to find the resultant force FR:
FR=√F21+F22
FR=√(10.788)2+(13.485)2=√116.3+181.5=√297.8≈17.26N
4. Calculate the Direction of the Resultant Force:
- The angle θ relative to the east can be found using:
tan(θ)=F1F2
tan(θ)=10.78813.485
θ=tan−1(0.799)≈38.66∘
- The direction of the resultant force is 38.66∘ south of east.
Final Answer:
The magnitude of the net electrostatic force acting on the charge at the center is approximately 17.26N and the direction is 38.66∘ south of east.
- Charge at the center (Q1): −3.00μC=−3.00×10−6C
- Charge due North (Q2): −4.00μC=−4.00×10−6C
- Charge due East (Q3): +5.00μC=+5.00×10−6C
- Radius of the compass (r): 0.100m
- Force due to Q2 (F1):
F1=k|Q1⋅Q2|r2
Where k=8.99×109N⋅m2/C2.
F1=8.99×109|−3.00×10−6⋅−4.00×10−6|(0.100)2
F1=8.99×10912.00×10−120.01=8.99×109⋅1.2×10−9=10.788N
This force acts towards the south (since both charges are negative).
F2=k|Q1⋅Q3|r2
F2=8.99×109|−3.00×10−6⋅5.00×10−6|(0.100)2
F2=8.99×10915.00×10−120.01=8.99×109⋅1.5×10−9=13.485N
This force acts towards the east (since the center charge is negative and the east charge is positive).
- The forces F1 and F2 are perpendicular to each other (south and east).
- We can use the Pythagorean theorem to find the resultant force FR:
FR=√F21+F22
FR=√(10.788)2+(13.485)2=√116.3+181.5=√297.8≈17.26N
- The angle θ relative to the east can be found using:
tan(θ)=F1F2
tan(θ)=10.78813.485
θ=tan−1(0.799)≈38.66∘
- The direction of the resultant force is 38.66∘ south of east.
The magnitude of the net electrostatic force acting on the charge at the center is approximately 17.26N and the direction is 38.66∘ south of east.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Linked Comprehension)5videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems63videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELASTICITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type1videos
ELECTRIC POTENTIAL
Similar Questions
There are two point charges +4 mu C and -2 mu C .The ratio of magnitude of electrostatic forces acting on them respectively will be
View SolutionEqual charges of +4μC are placed at the three corners of an equilateral triangle of side 2m. Calculate the magnitude and direction of the force on one of the charges.
View Solution
Knowledge Check
- Question 1 - Select One
A −4.0μC charge is located 0.30 m to the left of a + +6.0μC charge. What is the magnitude and direction of the electrostatic force on the positive charge ?
A2.4N to the rightB2.4N to the leftC4.8N to the rightD4.8N to the left - Question 2 - Select One
There are two charge +1μc and +2μc kept at certain separartion ,the ratio of electrostatic forces acting on them will be in the ratio
A1:2B2:1C1:1D1:4 - Question 3 - Select One
There are four charges, each with a magnitude of 2.0μC. Two are positive and two are negative. The charges are fixed to the corners of a 0.30 m square, one to a corner, in such a way that the net force on any charge is directed toward the center of the square. Find the magnitude of the net electrostatic force experienced by any charge.
A0.20 NB0.57 NC0.37 ND0.16 N
Three Charges of magnitude 100μC are placed at the corners A, Band C ofan equilateral triangle of side 4m. If the charge at A and Care positive and the one at point B is negative, what is the magnitude and direction of total force acting on charge at C? [5.625N]
View SolutionA particle of charge 3.00μC is separated by 0.120 m from a particle of charge −1.50μC. (a) What is the magnitude of the electrostatic force between them ? (b) What must their separation be to reduce that force by an order of magnitude ?
View SolutionIn Fig., the three particles are fixed in place and have charges q1=q2=+5e and q3=+2e. Distance a=3.00μm. What are the (a) magnitude and (b) direction of the net electric field at point P due to the particles ?
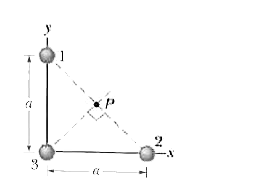 View Solution
View SolutionAssume that a honeybee is a sphere of diameter 1.000 cm with a charge +60.0pC uniformly spread over its surface . Assume also that a spherical pollen grain of diameter 40.0μC is electrically held on the surface of the bee because the bee's charge induces a charge of 1.00pC on the near side of the grain and a charge of 1+1.00pC on the far side. (a) what is the magnitude of the net electrostatic force on the grain due to the bee ? Next, assume that the bee brings the grain to a distance of 1.000 mm from the tip of a flower's stigma and that the tip is a particle of charge −60.0pC. (b) What is magnitude of the net electrostatic force on the grain due to the stigma ? (c ) Does the grain remain on the bee or move to the stigma ?
View SolutionA conducting spherical shell of outer radius R and inner radius r = 3R/4 has no net charge on it. At its center there is a point charge q, and at a distance 2R from its center there is a point charge Q (Fig.) . (a) What is the magnitude of the electrostatic force on the charge q at the center due to the shell ? (b) What is the magnitude of net force on it?
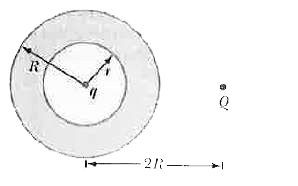 View Solution
View Solution

