Question

A charge particle A is fixed at the base of a uniform slope of inclination $\alpha$. Another charge particle B is placed on the slope at an angular position $\beta$ measured from the line of greatest slope passing through the position of the first particle. The coefficient of froction between the particle B and the slope is $\mu (\mu <\tan \alpha )$ .For the particle at B to stay in equilibrium what would be the maximum value of the angle $\beta$ ?

Explanation

The electrostatic repulsive froce will act along the line joining the two charges along AB. The driving force on particle B are `F_(e)` and mg sin `alpha`. The friction will act in the direction opposite to the resultant of these forces. Let friction act at an along `theta` to the line AB.
Let us analyze the force parallel and perpendicular to AB. the forces action on B perpendicular to AB are the cpmponents of friction force `f sin theta` and `(mg sin alpha) sin beta`.

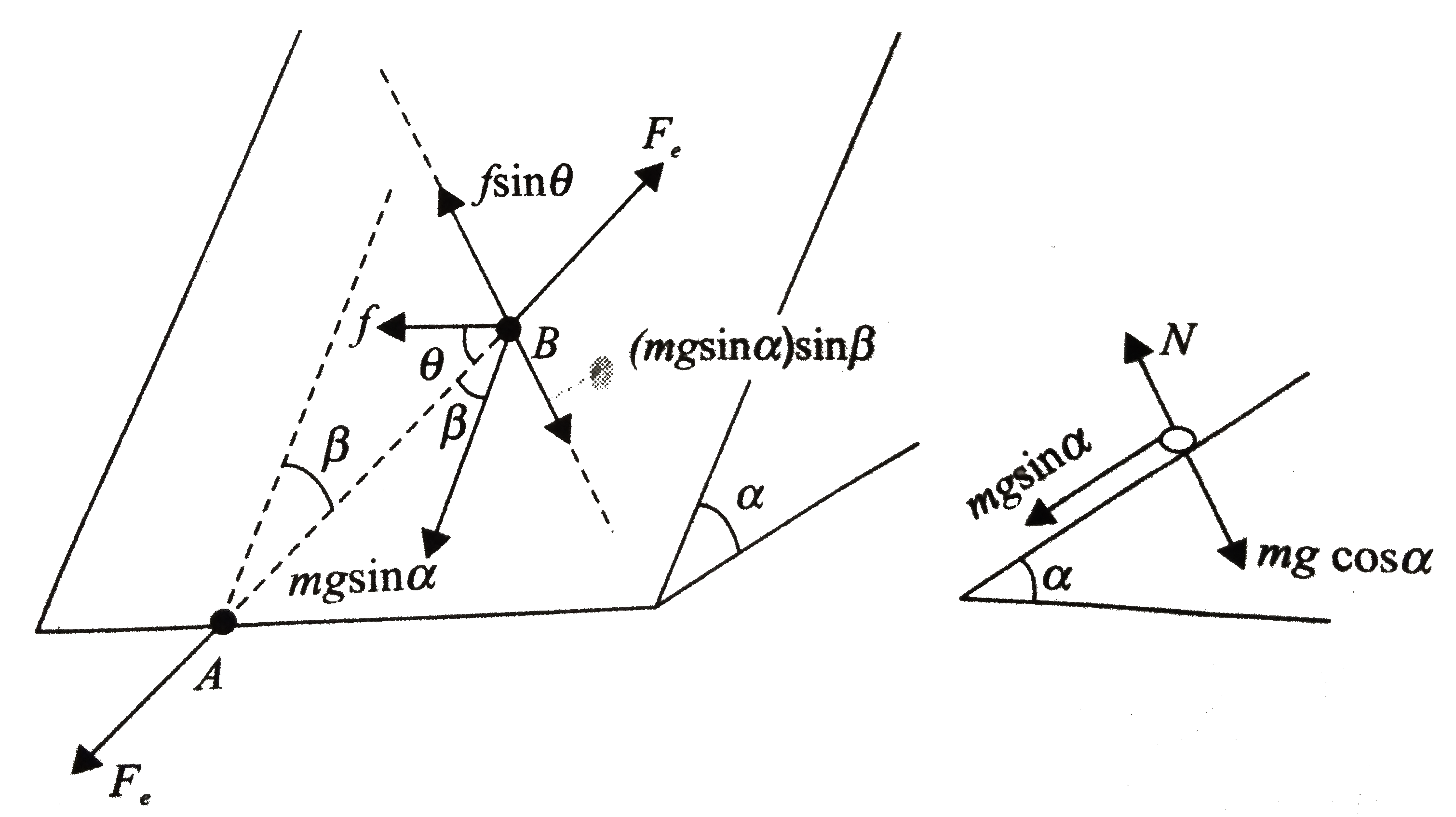
If the particle is in equilibrium
`f sin theta=(mg sin alpha) sin beta`
or `f= (mg sin alpha sin beta)/(sin theta)` or `f le mu mg cos alpha`
or, `(mg sin alpha sin beta)/(sin theta) le mu mg cos alpha`
or `sin beta le mu cot alpha xx sin theta`
`beta` is maximum when `sin theta=1`. So
`beta le sin^(-1)(mu cot alpha)`.