A charge +Q is uniformly distributed in a spherical volume of radius R. A particle of charge +q and mass m projected with velocity v0 the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of v0 such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is
√Qq2πε0mR
√Qqπε0mR
√2Qqπε0mR
√Qq4πε0mR
The correct Answer is:D
Ui+Ki=Uf+kf
orqVi+12mv2min=qVf+0
=orq(14πε0)(QR)+12mv2min+q[32×Q4πε0R]
from here we can find vmin
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
A charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

View Solution
Knowledge Check
Charge q is uniformly distributed on a disc of radius r. If the disc is rotated with a frequency v, then magnetic field induction at the centre will be
Aμ0qvrBμ0qvrCμ0vqrDμ0qvrA charge q0 is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
Aq04ε0Bq02ε0Cq03ε0Dq0ε0A bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
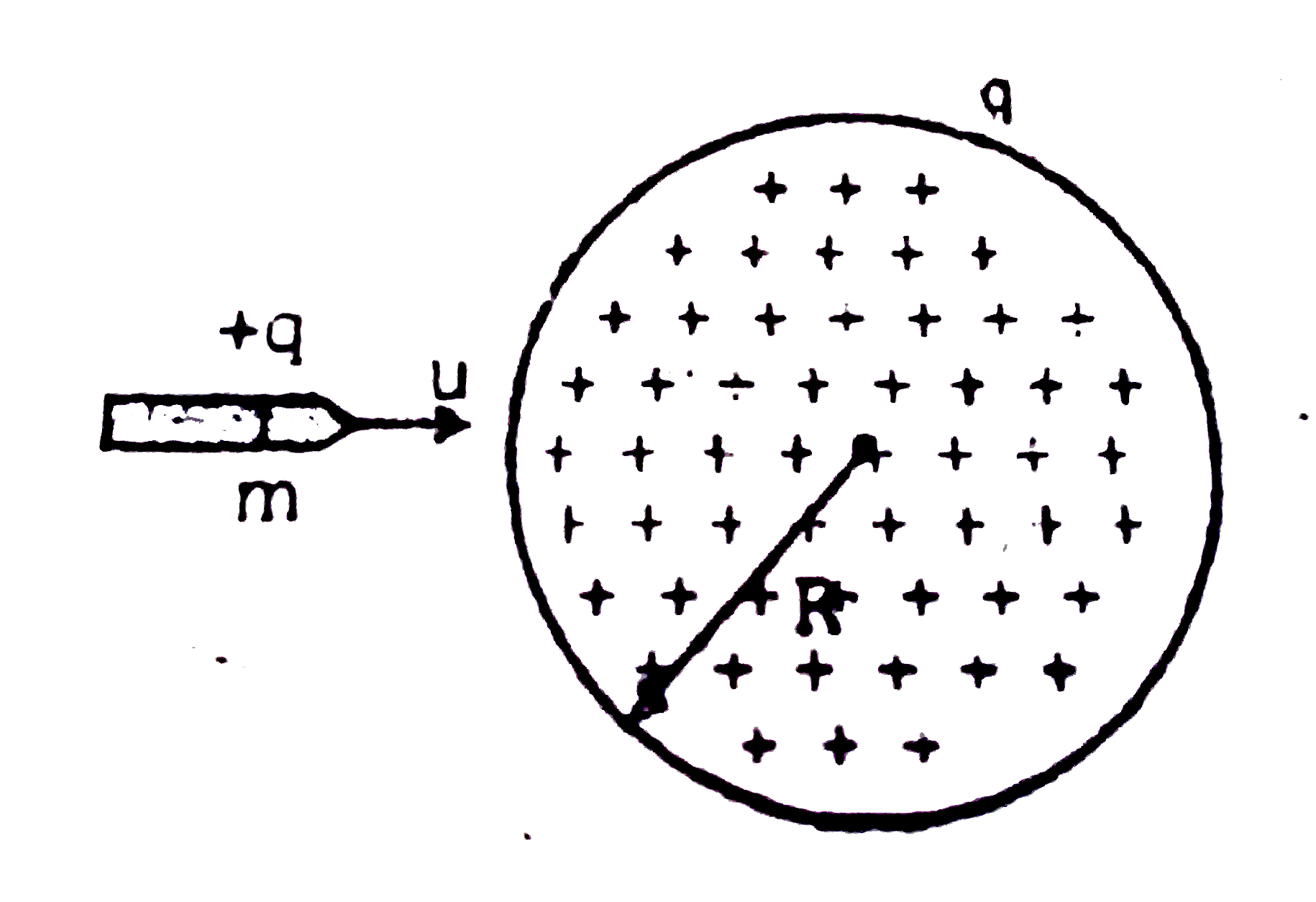 Aq√2πε0mRBq√4πε0mRCq√8πε0mRD√3q√4πε0mR
Aq√2πε0mRBq√4πε0mRCq√8πε0mRD√3q√4πε0mR
A charge q is uniformly distributed over the volume of a shpere of radius R. Assuming the permittively to be equal to unity throughout, find the potential
(a) at the centre of the sphere,
(b) inside the sphere as a function of the distance r from its centre.
View SolutionA charge "Q" of mass "m" is at rest on a smooth horizontal plane.Another identical particle is projected with a velocity v towards it from long distance then
View SolutionA charge Q is uniformly distributed over the surface of two conducting concentric spheres of radii R and r (Rgtr). Then, potential at common centre of these spheres is
View SolutionA unit positive point charge of mass m is projected with a velocity v inside the tunnel as shown. The tunnel has been made inside a uniformly charged nonconducting sphere. The minimum velocity with which the point charge should be projected such it can it reach the opposite end of the tunnel is equal to
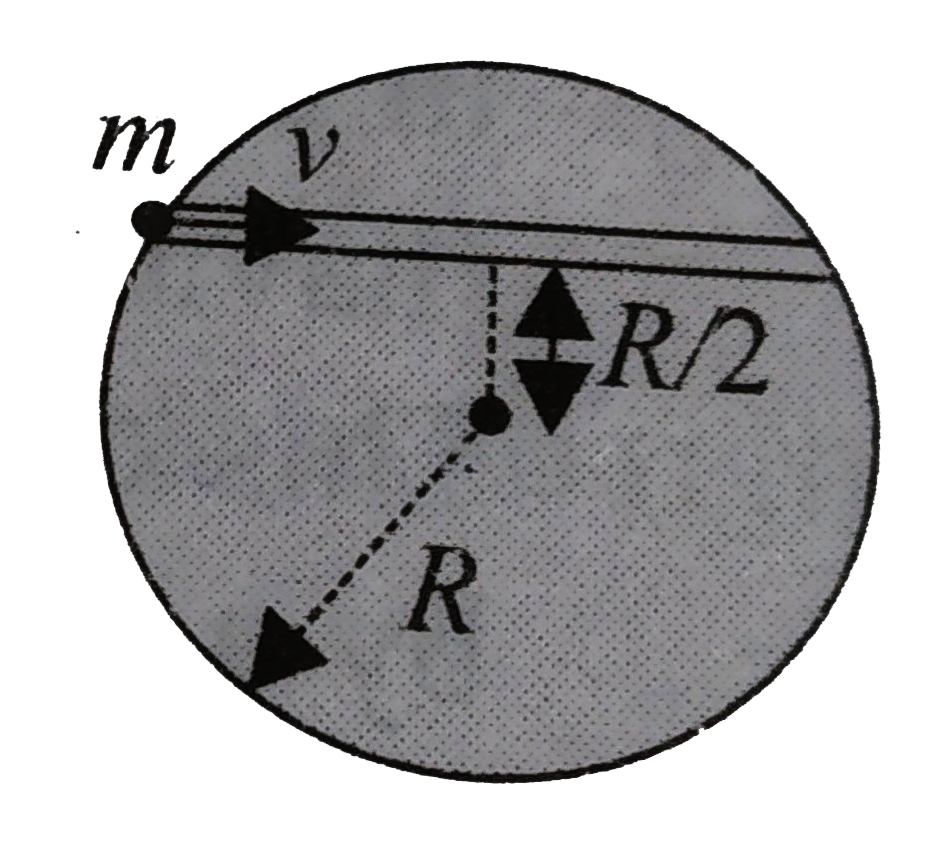
View SolutionA unit positive point charge of mass m is projected with a velocity v inside the tummel as shown. The tunnel has been made inside a uniformly charged non conducting sphere. The minimum velocity with which the point charge should be projected such that it can it reach the opposite end of the tunnel, is equal to:

View Solution
