A charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
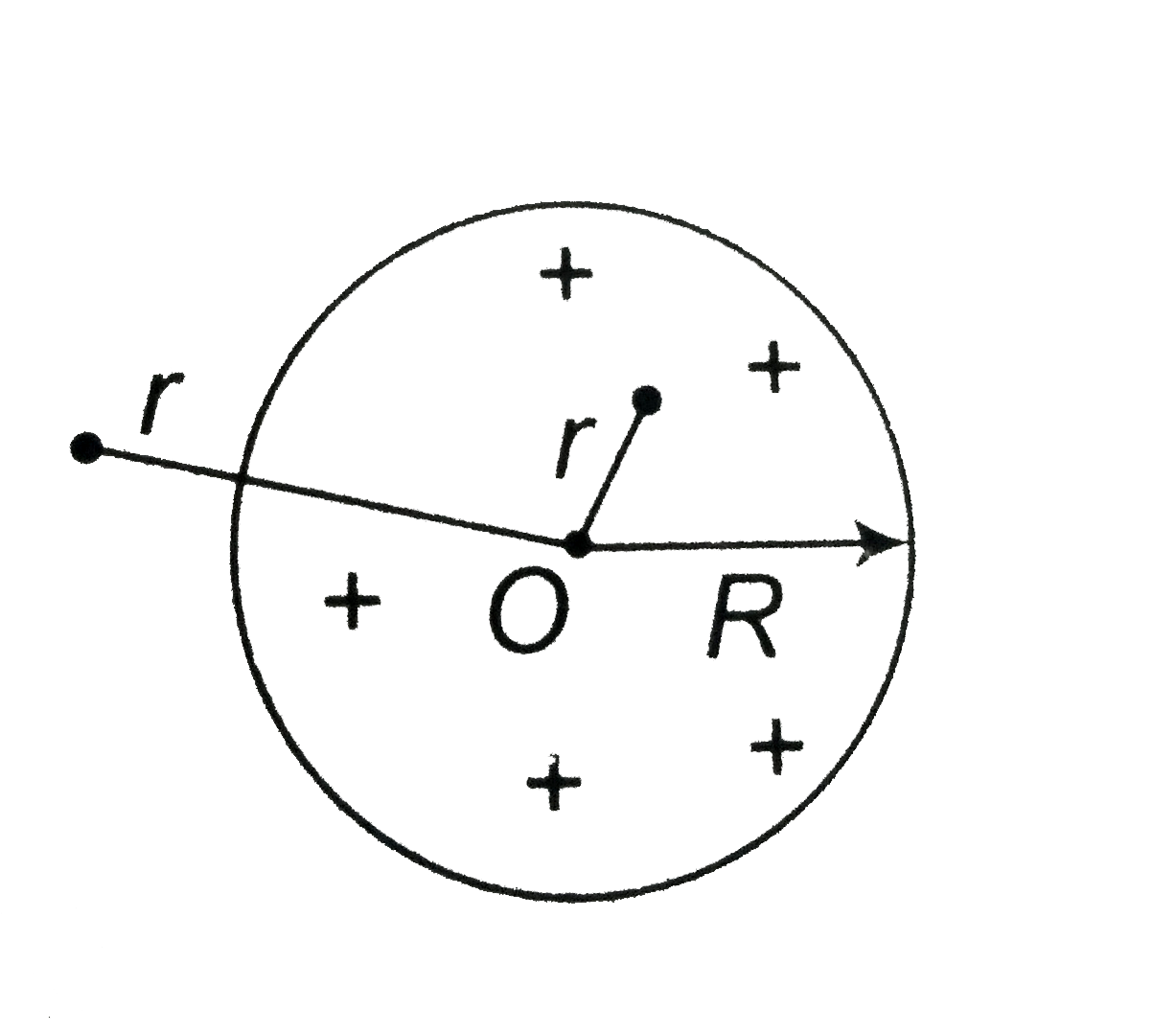
Inside (r>R)
E=14π∈0.QrR3
dV=4πr2dr
dU=udV=12∈0E2dV
=12∈0(14π∈0.QrR3)24πr2dr
U∈=Q28π∈0R6∫R0r4dr=Q28π∈0R6R55
=Q240π∈0R
Outside (r>R)
Uout=Q28π∈0R (as proved in the previous example)
U=U∈+Uout
=3Q220π∈0R=14π∈0.3Q220π∈0R=14π∈0.3Q25R
If we want to calculate energy stored in a spherical shell of inner radius R and outer radius 2R.
U=∫2RR12∈0(14π∈0Qr2)24πr2dr
=Q28π∈0∫2RRr−2dr=Q216π∈0R
Topper's Solved these Questions
Similar Questions
Find the electric potential energy of a uniformly charged sphere.
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
View Solution
Knowledge Check
A charge −Q is unformly distributed over a non-conducting semi-circular rod of radius R. The potential at the center is
A0B−Q4πε0RCQ4πε0(2R)D2Q4πε0RA charge Q is uniformly distributed only on the fourths portion of a ring of radius R. The elctric potential at centre of ring is
A3Q4πε0RBQ4πε0RC3Q2πε0RD6Q4πε0RA charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?
 A
A B
B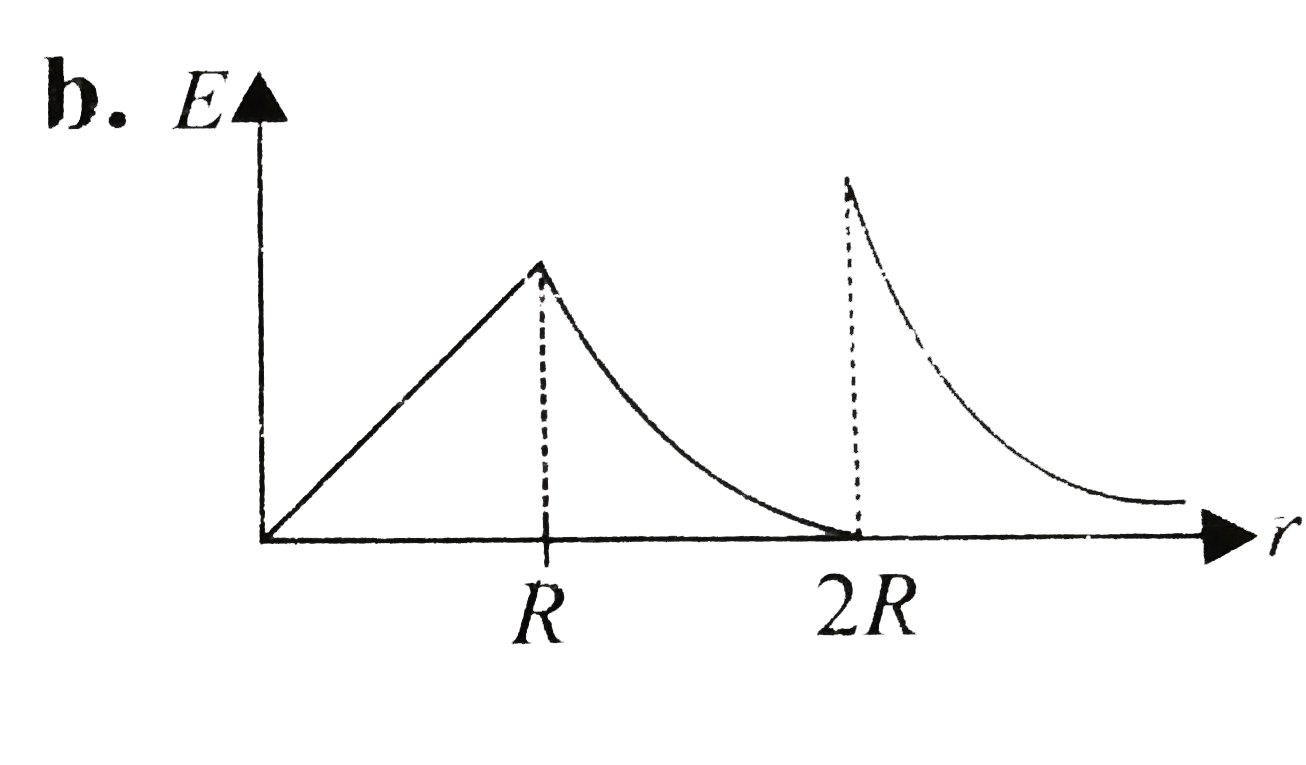 C
C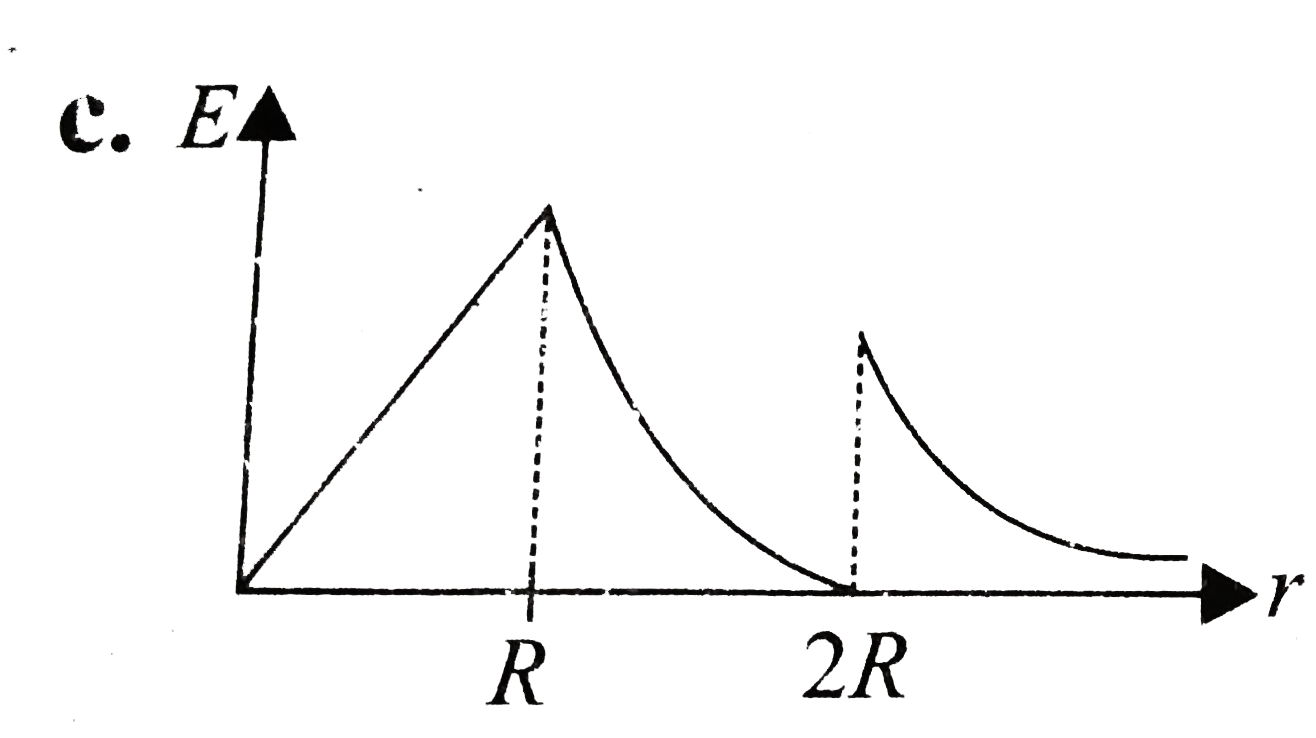 D
D
There is a hemispherical shell having charge Q uniformly distributed on its surface. Radius of the shell is R. Find electric potential and field at the centre (of the sphere).
View SolutionA charge Q is uniformly distributed over the surface of two conducting concentric spheres of radii R and r (Rgtr). Then, potential at common centre of these spheres is
View SolutionA charge Q is distribution over a metal sphere of radius R. What is the electric field and electric potential at the centre ?
View SolutionThe electric potential inside a conducting sphere
View SolutionCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View Solution
