A charge q is uniformly distributed over the volume of a shpere of radius R. Assuming the permittively to be equal to unity throughout, find the potential
(a) at the centre of the sphere,
(b) inside the sphere as a function of the distance r from its centre.
From Gauss' theorem intensity at a point, inside the sphere at a distance r from the centre is given by, Er=ρr3ε0 and outside it, given by Er=14πε0qr2
(a) Potential at the centre of the sphere,
φ0=∫∞0→E.→dr=∫R0ρr3ε0dr+∫∞Rq4πε0r2dr=ρ3εR22+q4πε0R
as =q8πε0R+q4πε0R=3q8πε0R (as ρ=3q4πR3)
(b) Now, potential at any point, inside the sphere, at a distance r from it s centre.
φ(r)=∫Rrρ3ε0rdr∫∞rq4πε0drr2
On intergation :φ(r)=3q8πε0R[1r23R2]=φ0[1−r23R2]
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field
47 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

View Solution
Knowledge Check
A solid sphere of radius R has charge q uniformly distributed over its volume. The distance from it surfce at which the electrostatic potential is equal to half of the potential at the centre is
ARB2RCR3DR2→E due to uniformly charged sphere of radius R as a function of distance from its centre is represented by:
A B
B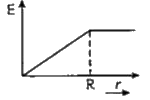 C
C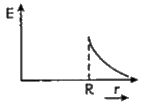 D
D
→E due to uniformly charged sphere of radius R as a function of distance from its centre is represented by
A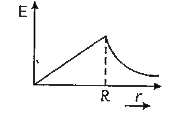 B
B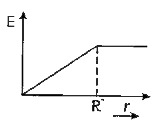 C
C D
D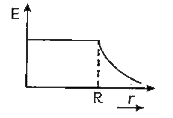
A charge Q is uniformly distributed over the surface of two conducting concentric spheres of radii R and r (Rgtr). Then, potential at common centre of these spheres is
View SolutionA charge Q is distribution over a metal sphere of radius R. What is the electric field and electric potential at the centre ?
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and R(>r) such that the surface charge densities are equal. Find the potential at the common centre.
View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and R(>r) such that the surface charge densities are equal. Find the potential at the common centre.
View Solution
