A charged particle begins to move from the origin in a region which has a uniform magnetic field in the x-direction and a uniform electric field in the y-direction. Its speed is v when it reaches the point (x, y, z). Then, v will depend
only on x
only on y
on both x and y, but not z
on x,y and z
The correct Answer is:b
To solve the problem step by step, we need to analyze the motion of a charged particle in the presence of both electric and magnetic fields.
Step 1: Understanding the Fields
The problem states that there is a uniform magnetic field in the x-direction and a uniform electric field in the y-direction. We can denote these fields as:
- Magnetic Field, B = B₀ i (where i is the unit vector in the x-direction)
- Electric Field, E = E₀ j (where j is the unit vector in the y-direction)
Step 2: Analyzing the Forces
A charged particle (with charge Q) moving in these fields will experience forces due to both fields:
- The force due to the electric field is given by F_E = Q E = Q E₀ j.
- The force due to the magnetic field is given by F_B = Q (v × B). However, since the magnetic field is in the x-direction and the particle's motion is in the y-direction, the magnetic force will not do work on the particle. The magnetic force only changes the direction of the velocity, not its magnitude.
Step 3: Work Done on the Particle
Since the magnetic force does no work, the work done on the particle is solely due to the electric field. The work done by the electric field when the particle moves a distance s in the direction of the electric field is:
- W = F_E · s = Q E₀ s.
Step 4: Relating Work Done to Kinetic Energy
According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy:
- W = ΔKE = KE_final - KE_initial.
Assuming the particle starts from rest, the initial kinetic energy is zero, so:
- W = KE_final = (1/2) m v².
Step 5: Setting Up the Equation
From the above relationships, we can equate the work done to the change in kinetic energy:
- Q E₀ s = (1/2) m v².
Step 6: Solving for Velocity
From the equation, we can express the speed v in terms of the distance s:
- v² = (2 Q E₀ s) / m.
- v = √((2 Q E₀ s) / m).
Step 7: Conclusion
The speed v of the charged particle when it reaches the point (x, y, z) depends on the distance s it has moved in the direction of the electric field (which is the y-direction).
Final Answer
Thus, the speed v will depend on the distance s traveled in the direction of the electric field.
---
The problem states that there is a uniform magnetic field in the x-direction and a uniform electric field in the y-direction. We can denote these fields as:
- Magnetic Field, B = B₀ i (where i is the unit vector in the x-direction)
- Electric Field, E = E₀ j (where j is the unit vector in the y-direction)
A charged particle (with charge Q) moving in these fields will experience forces due to both fields:
- The force due to the electric field is given by F_E = Q E = Q E₀ j.
- The force due to the magnetic field is given by F_B = Q (v × B). However, since the magnetic field is in the x-direction and the particle's motion is in the y-direction, the magnetic force will not do work on the particle. The magnetic force only changes the direction of the velocity, not its magnitude.
Since the magnetic force does no work, the work done on the particle is solely due to the electric field. The work done by the electric field when the particle moves a distance s in the direction of the electric field is:
- W = F_E · s = Q E₀ s.
According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy:
- W = ΔKE = KE_final - KE_initial.
Assuming the particle starts from rest, the initial kinetic energy is zero, so:
- W = KE_final = (1/2) m v².
From the above relationships, we can equate the work done to the change in kinetic energy:
- Q E₀ s = (1/2) m v².
From the equation, we can express the speed v in terms of the distance s:
- v² = (2 Q E₀ s) / m.
- v = √((2 Q E₀ s) / m).
The speed v of the charged particle when it reaches the point (x, y, z) depends on the distance s it has moved in the direction of the electric field (which is the y-direction).
Thus, the speed v will depend on the distance s traveled in the direction of the electric field.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
When a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionA particle moves in a region having a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be
View SolutionA charged particle moves in a circular path in a uniform magnetic field. If its speed is reduced, then its tiem period will
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).
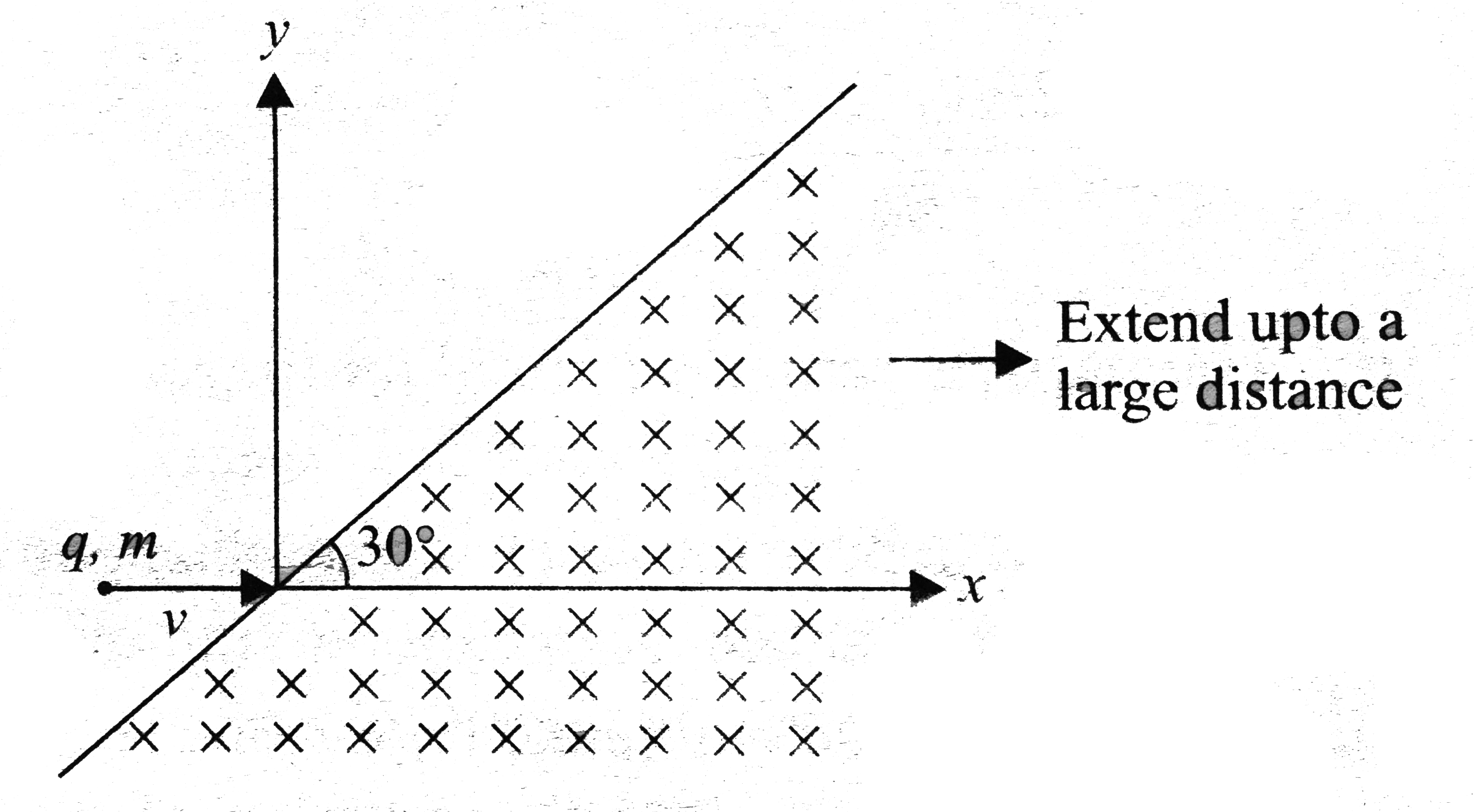
View SolutionA charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other . The particle will remove in a
View SolutionA charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other . The particle will remove in a
View SolutionA positively charged particle moving due east enters a region of uniform magnetic field directed vertically upwards. The partical will be
View SolutionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View SolutionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View Solution
