A charged particle is projected in a magnetic field of (5ˆI+9ˆj)mT and its acceleration is found to be (9ˆI−xˆj)×10−6m/s2. What should be the value of x?
We know that magnetic force is always perpendicular
to the magnetic field. So the acceleration vector must also be perpendicular to the magnetic field. The dot product of two mutually perpendicular vectors should be zero hence we get the following:
→a⋅→B=0⇒(5ˆi+9ˆj)⋅(9ˆi−xˆj)×10−6×10−3=0
⇒45−9x=0⇒x=5
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Very Short Answer Questions )59videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Additional Questions )16videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) (Short Answer Type Questions )6videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
Charged particle is projected in a magnetic field of (7ˆi−3ˆj)times10−3T . The acceleration of the particle is found to be (xˆi+7ˆj)times10−3msec2 .The value of x is
View SolutionCharged particle is projected in a magnetic field of (7ˆi−3ˆj)×10−3T .The acceleration of the particle is found to be (xˆi+7ˆj)×10−3msec2.The value of x is
View Solution
Knowledge Check
- Question 1 - Select One
A particle is moving in x-y plane. At an instant, it has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2 At that instant, the radius of curvature of its path will be :
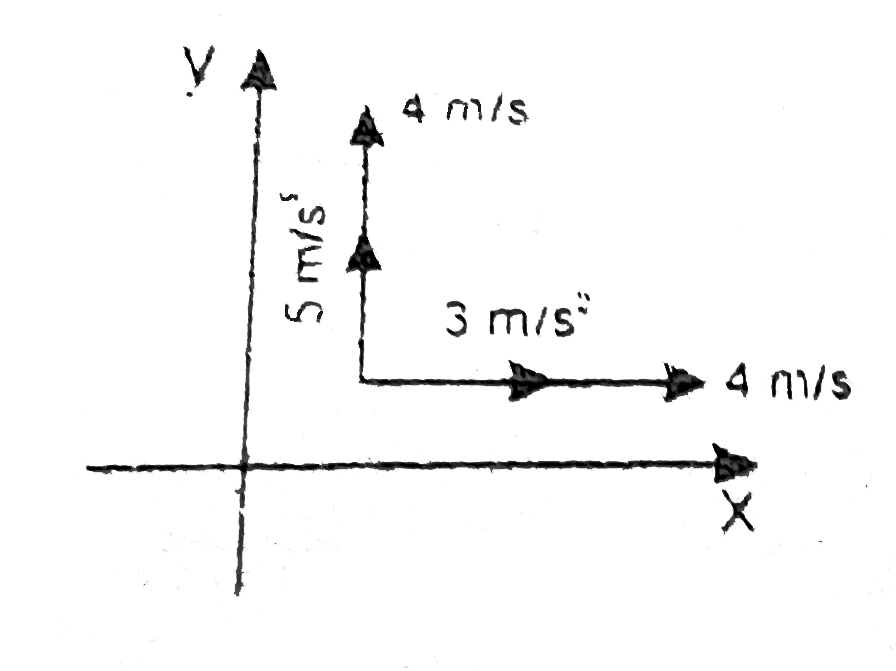 A16√2mB15 mC18 mDNon of these
A16√2mB15 mC18 mDNon of these
A point charge +q0 is projected in a magnetic field →B=(ˆi+2ˆj−3ˆk). If acceleration of the particle is →a=(2ˆi+bˆj+ˆk) then value of b will be
View SolutionA point charge +q0 is projected in a magnetic field →B=(ˆi+2ˆj−3ˆk). If acceleration of the particle is →a=(2ˆi+bˆj−ˆk) then value of b will be
View SolutionA charged particle has acceleration →a=2ˆi+xˆj in a megnetic field →B=−3ˆi+2ˆj−4ˆk. Find the value of x.
View SolutionA charged particle has acceleration →a=2ˆi+xˆj in a megnetic field →B=−3ˆi+2ˆj−4ˆk. Find the value of x.
View SolutionA charged particle moving in a magnetic field →B=ˆi−ˆj tesla, has an acceleration of 2ˆi+αˆj at some instant. Find the value of α
View SolutionA charged particle moving in a magnetic field →B=ˆi−ˆj tesla, has an acceleration of 2ˆi+αˆj at some instant. Find the value of α
View SolutionA particle is moving in x-y plane. At an instant, it has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2 At that instant, the radius of curvature of its path will be :
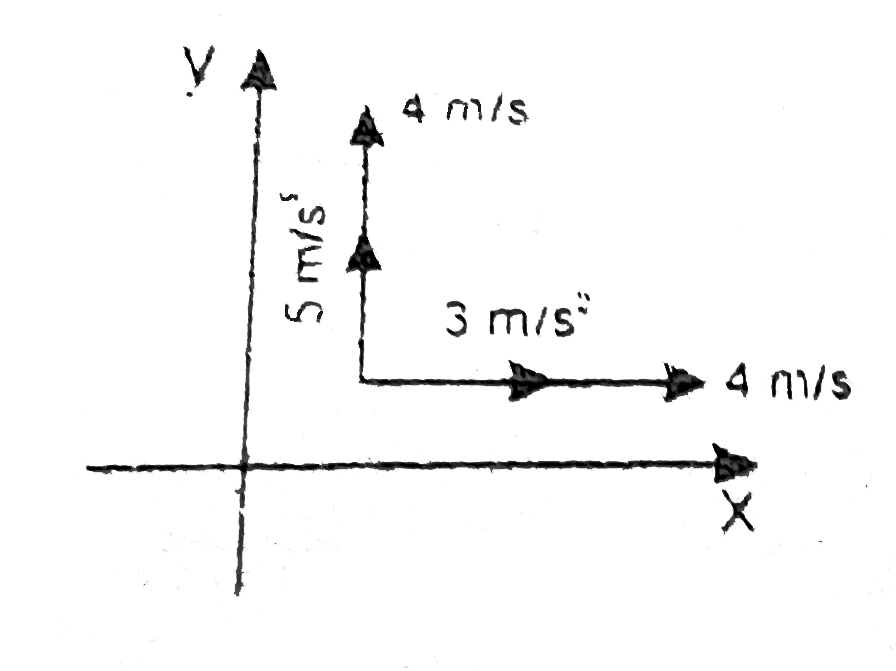 View Solution
View Solution

