A circular coil has a resistance of 40Ω. Two points P and Q of the coil, which are one quarter of the circumference apart are connected to a 16 V battery, having an internal resistance of 0.5Ω ? What is the main current flowing in the circuit ?
0.5 A
1A
2A
3A
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Determine the resistances of the segments of the coil
The total resistance of the coil is given as R=40Ω. Since points P and Q are one quarter of the circumference apart, we can divide the total resistance into two parts:
- R1 (the resistance between points P and Q) will be R4=40Ω4=10Ω
- R2 (the remaining part of the coil) will be R−R1=40Ω−10Ω=30Ω
Step 2: Calculate the equivalent resistance of the circuit
The resistances R1 and R2 are in parallel with the internal resistance of the battery r=0.5Ω. The formula for the equivalent resistance Req of two resistors in parallel is given by:
1Req=1R1+1R2
Substituting the values:
1Req=110+130
Finding a common denominator (which is 30):
1Req=330+130=430=215
Thus,
Req=152=7.5Ω
Step 3: Find the total resistance in the circuit
Now, we need to add the internal resistance of the battery to the equivalent resistance:
Rtotal=Req+r=7.5Ω+0.5Ω=8Ω
Step 4: Calculate the current using Ohm's Law
Using Ohm's Law, V=I⋅R, we can find the current I:
I=VRtotal=16V8Ω=2A
Final Answer
The main current flowing in the circuit is 2A.
---
The total resistance of the coil is given as R=40Ω. Since points P and Q are one quarter of the circumference apart, we can divide the total resistance into two parts:
- R1 (the resistance between points P and Q) will be R4=40Ω4=10Ω
- R2 (the remaining part of the coil) will be R−R1=40Ω−10Ω=30Ω
The resistances R1 and R2 are in parallel with the internal resistance of the battery r=0.5Ω. The formula for the equivalent resistance Req of two resistors in parallel is given by:
1Req=1R1+1R2
Substituting the values:
1Req=110+130
Finding a common denominator (which is 30):
1Req=330+130=430=215
Thus,
Req=152=7.5Ω
Now, we need to add the internal resistance of the battery to the equivalent resistance:
Rtotal=Req+r=7.5Ω+0.5Ω=8Ω
Using Ohm's Law, V=I⋅R, we can find the current I:
I=VRtotal=16V8Ω=2A
The main current flowing in the circuit is 2A.
Topper's Solved these Questions
Similar Questions
A certain length of a uniform wire of resistance 12Ω is bent into a circle and two points, a quarter of circumference apart, are connected to a battery of emf 4 V and internal resistance 1Ω. Find the current in the different parts of the circuit.
View SolutionA certain length of a uniform wire of resistance 12Ω is bent into a circle and two points, a quarter of circumference apart, are connected to a battery of emf 4 V and internal resistance 1Ω. Find the current in the different parts of the circuit.
View Solution
Knowledge Check
- Question 1 - Select One
A series combination of two resistors 1Ω each is connected to a 12 V battery of internal resistance 0.4Ω. The current flowing through it will be
A3.5AB5AC6AD10A - Question 2 - Select One
Two resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing thrpough the battery ?
A4AB43AC417AD1A - Question 3 - Select One
A wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are
 A623A and 1823AB526A and 1526AC425A and 1225AD325A and 925A
A623A and 1823AB526A and 1526AC425A and 1225AD325A and 925A
in the circuit shown in the figure, each battery is of 5 V and has an internal resistance of 0.2 Omega What is the reading of the ideal voltmeter V
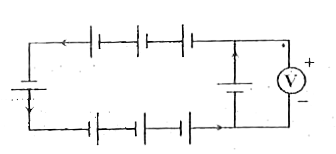 View Solution
View SolutionA wire of resistance 4Ω is connected to a battery having an internal resistance of 1Ω For a current of 6 A to flow through the circuit what should be the emf of the battery ?
View SolutionA 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38 Ω as shown in the Fig. Find the value of the current in circuit.
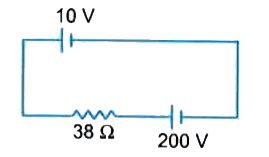 View Solution
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.
 View Solution
View SolutionShows a network of eight resistors battery of resistance R(=2Ω) connected in a 3V battery of negligible internal resistance. The current I in the circuit is
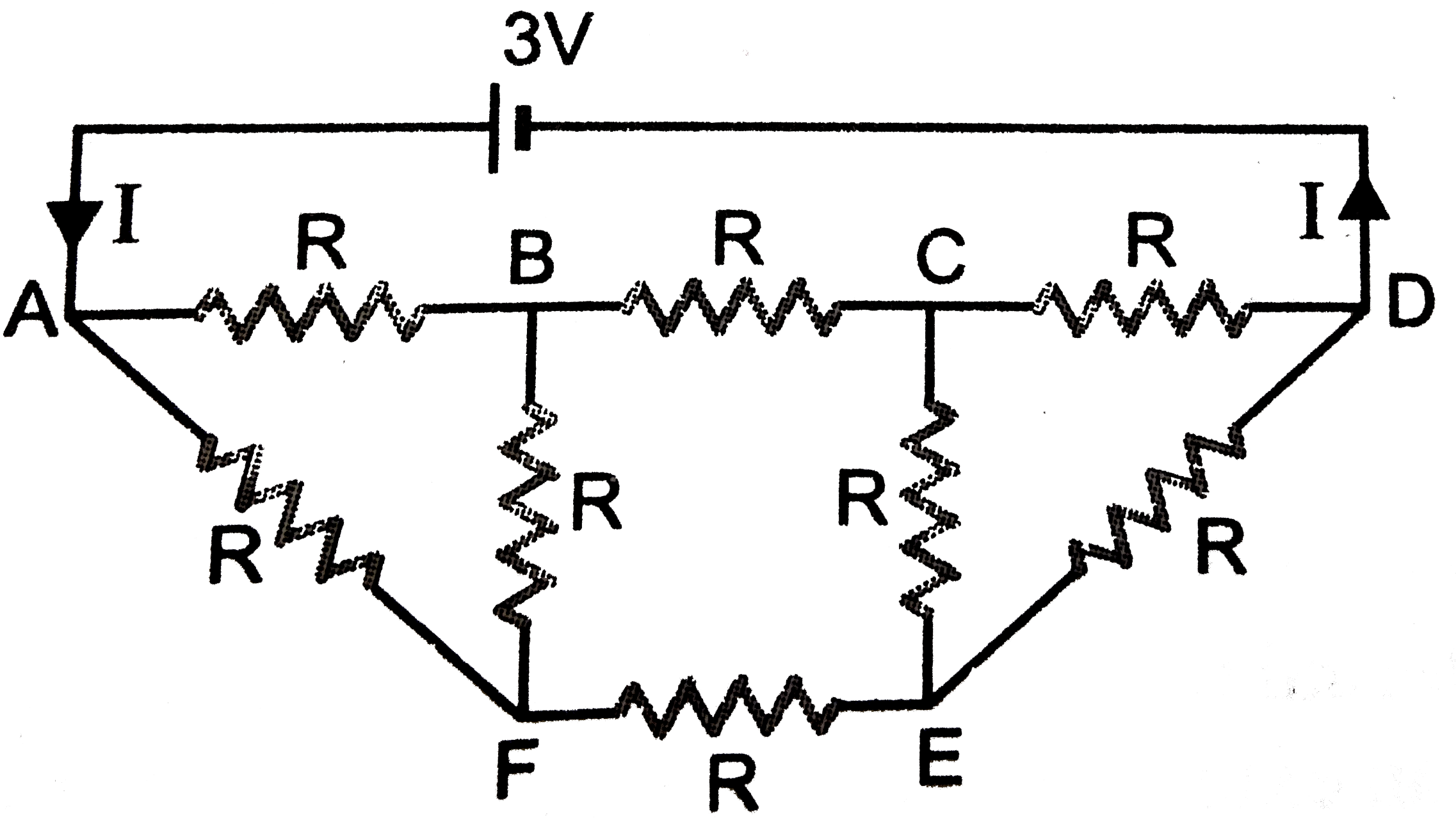 View Solution
View Solution

