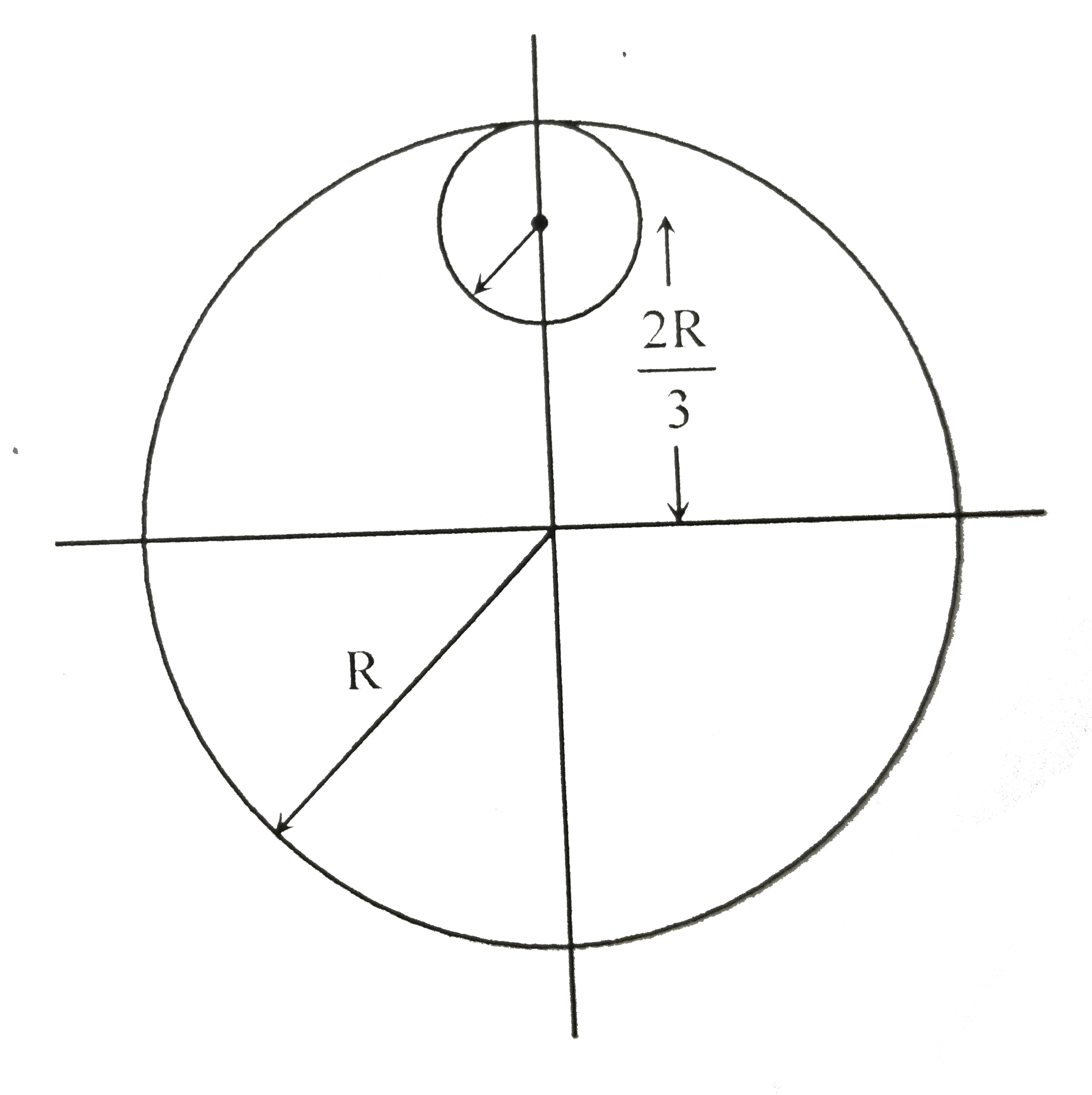
A circular disc of mass 9m, has a hole of radius R/3, cut from it as shown in given figure. The moment of inertia of the remaining part of the disc about the axis passing through the centre of the disc and perpendicular to its plane will be :

379mR2
409mR2
4mR2
8mR2
The correct Answer is:C
Mass per unit area of the disc σ=9mπR2
∴ Mass of removed disc M=σ={π(R3)2}=9mπR2.πR29=m
Moment of inertia of second disc about the given axis (From theorem of parallel axis)
I.=12m(R3)2+m(2R3)2
=12m(R29)+m(4R29)=mR22
Moment of inertia of remaining part = Moment of inertia of complete disc - Moment of inertia of removed disc
=12(9mR2)−mR22=4mR2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - LEVEL-III (MCQ)
10 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- RAY OPTICSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION
32 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test
28 Videos
Similar Questions
A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View Solution
Knowledge Check
If a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
Amoment of inertia decreasesBmoment of inertia increasesCradius of gyration increasesDradius of gyration decreasesFrom a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
A circular of radius R has mass 9m . A hole of radius R3 is cut from it as shown in figure. The moment of inertia of the remaining part about an axis passing through centre 0 of the disc and perpendicular of the plane of disc is xmR2 .Find value of x
View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionCalculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis through the centre of the disc and perpendicular to its plane
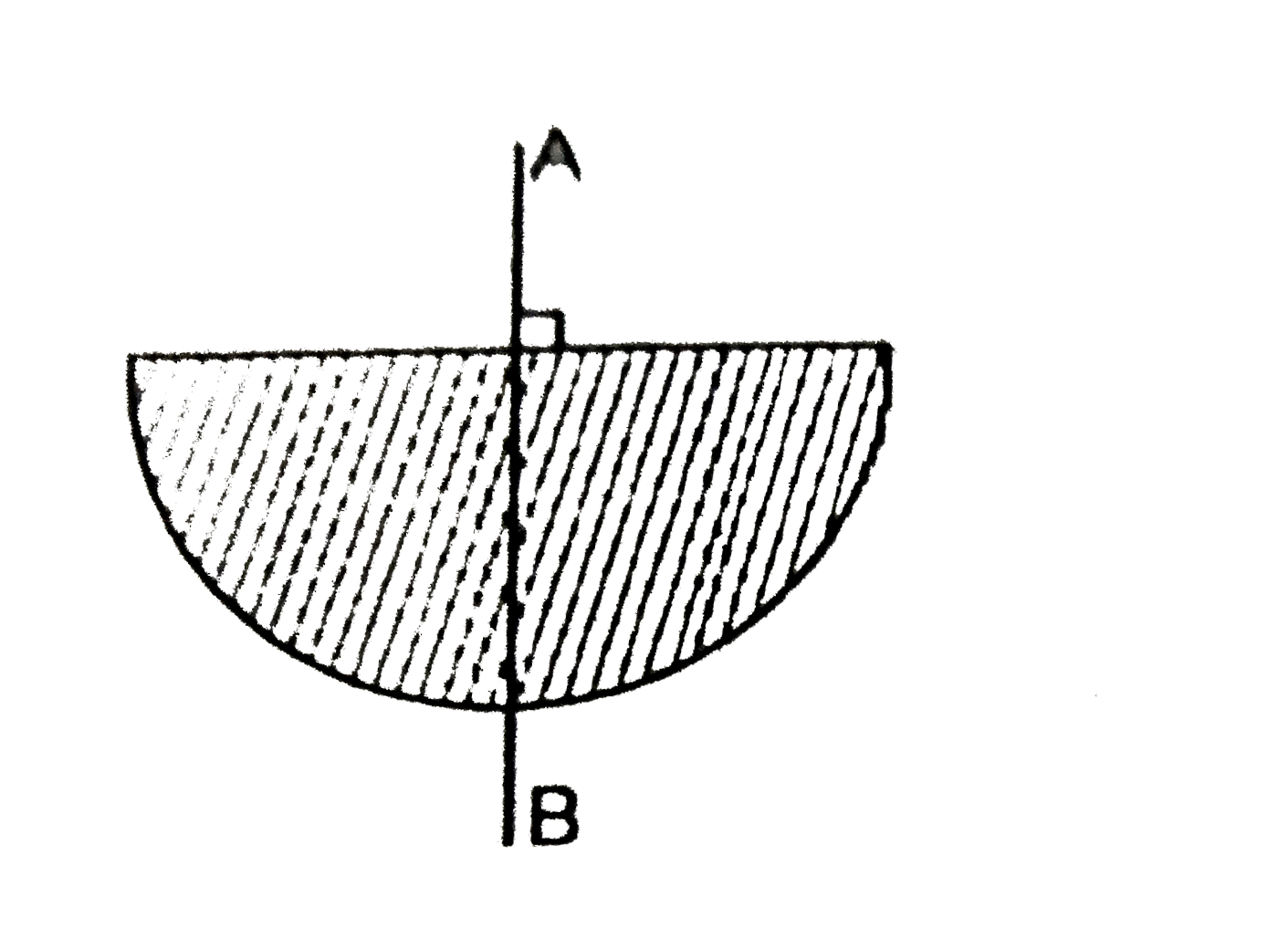
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
View Solution
