A circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. △K/Ki
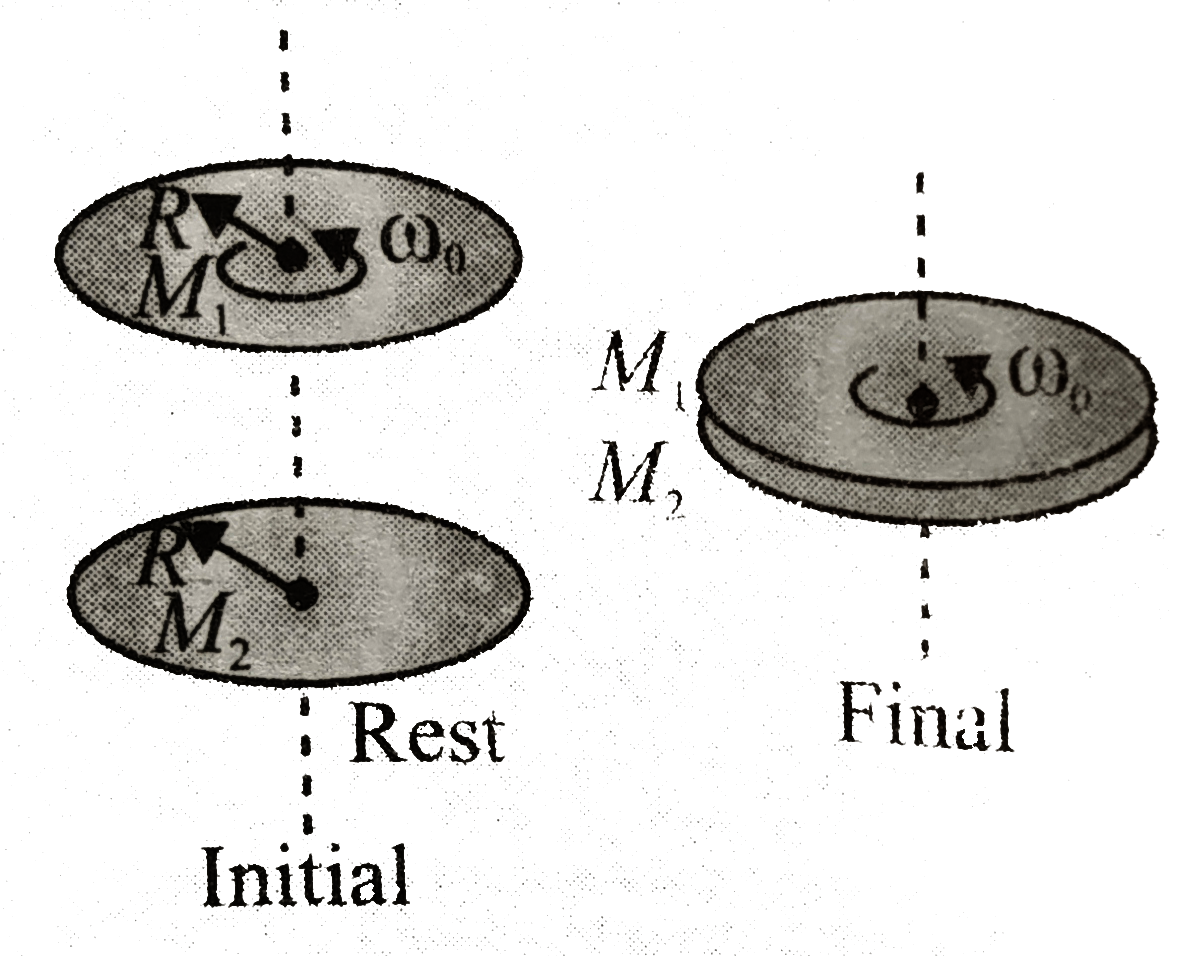
The frictional force between the two discs exerts a retarding torque on M1 and an accelerating torque on M2. Till both the discs start moving together with a common angular speed ω, the angular momentum of each disc changes but the angular momentum o the whole system (M1+M2) remains conserved as there is no torque acint on the system.
A rotating disc is gently placed on a momentum, we get
Li=Lf
(M1R22)ω0=(M1R22+M2R22)ω
ω=M1ω0M1+M2
b. The work done by frictioln done by friction is equal to te change in kinetic energy of the system.
Wf=Kf−Ki
Ki=12I1ω20=12(M1R22)ω20=14M1R2ω20
Kf=12(I1+I2)ω2=12(M1+M2)R22[M1ω0M1+M2]2
=14M21(M1+M2)R2ω22
Wf=Kf−Ki=−14(M1+M2M1+M2)R2ω20
Note that the negative sign shows that work done by friction reduces the kinetic energy of the system.
c. The fractional loss in kinetic energy is
△KKi=M2M1+M2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.3
21 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View Solution
Knowledge Check
A circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
A10 JB6 JC2 JD4 JA circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. △K/Ki
 Am1m2Bm2m1+m2Cm2m1Dm1m1+m2
Am1m2Bm2m1+m2Cm2m1Dm1m1+m2A uniform disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to its plane with an angular velocity ω. Another disc of mass M/3 and radius R/2 is placed gently on the first disc coaxial. Then final angular velocity of the system is
A12ω/13B13ω/12C3ω/4D11ω/12
A disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

View SolutionA circular disc of mass M and radius R rotating with speed of ω and another disc of same mass M and radius R/2 placed co axially on first disc, after sometime disc-2 also attain constant speed w2 . Find loss of percentage in energy
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
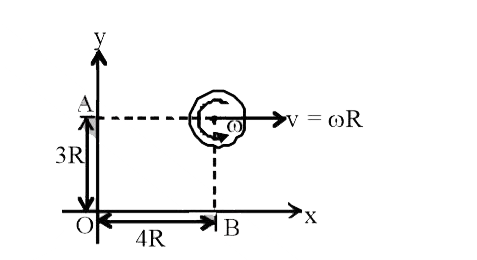
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

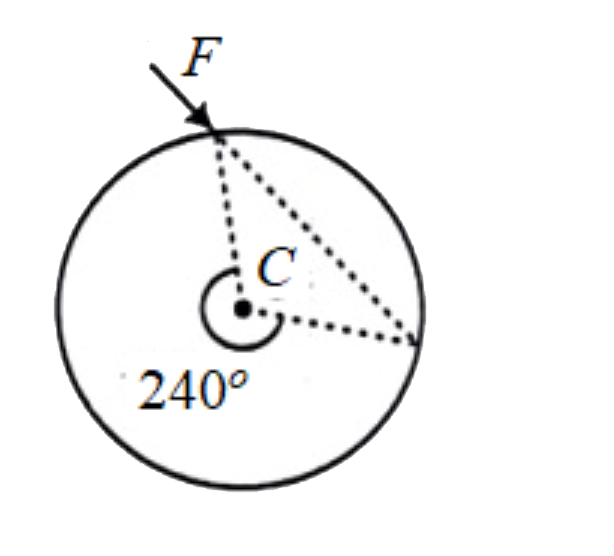
View SolutionA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
View Solution
