A circular plate of radius 2 cm is kept at a distance of 22 cm in front of a concave mirror. The focal length of mirror is 10 cm. Calculate the perimeter of image formed if plate is kept coaxially to the principal axis.
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given values
- Radius of the circular plate (r) = 2 cm
- Distance of the plate from the mirror (u) = -22 cm (negative because it is in front of the mirror)
- Focal length of the concave mirror (f) = -10 cm (negative for concave mirrors)
Step 2: Use the mirror formula to find the image distance (v)
The mirror formula is given by:
1f=1v+1u
Rearranging this gives:
1v=1f−1u
Substituting the values of f and u:
1v=1−10−1−22
Calculating the right side:
1v=−110+122
Finding a common denominator (which is 110):
1v=−11110+5110=−6110=−355
Thus,
v=−553 cm
Step 3: Calculate the radius of the image using magnification
The magnification (m) is given by:
m=height of imageheight of object=−vu
Here, we consider the height of the object as the radius of the circular plate (2 cm). Thus:
m=−−553−22
Calculating this gives:
m=553×22=5566=56
Now, the radius of the image (R) can be found as:
R=m×r=56×2=106=53 cm
Step 4: Calculate the perimeter of the image
The perimeter (P) of a circle is given by:
P=2πR
Substituting the value of R:
P=2×227×53
Calculating this gives:
P=22021 cm
Final Answer
The perimeter of the image formed is:
22021 cm
---
- Radius of the circular plate (r) = 2 cm
- Distance of the plate from the mirror (u) = -22 cm (negative because it is in front of the mirror)
- Focal length of the concave mirror (f) = -10 cm (negative for concave mirrors)
The mirror formula is given by:
1f=1v+1u
Rearranging this gives:
1v=1f−1u
Substituting the values of f and u:
1v=1−10−1−22
Calculating the right side:
1v=−110+122
Finding a common denominator (which is 110):
1v=−11110+5110=−6110=−355
Thus,
v=−553 cm
The magnification (m) is given by:
m=height of imageheight of object=−vu
Here, we consider the height of the object as the radius of the circular plate (2 cm). Thus:
m=−−553−22
Calculating this gives:
m=553×22=5566=56
Now, the radius of the image (R) can be found as:
R=m×r=56×2=106=53 cm
The perimeter (P) of a circle is given by:
P=2πR
Substituting the value of R:
P=2×227×53
Calculating this gives:
P=22021 cm
The perimeter of the image formed is:
22021 cm
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (2)
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (3)
18 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
An object is kept at a distance os 5 cm in front of a convex mirror of focal lentgth 10 cm. Calculate the position and magnigication of the image and state nature.
View SolutionAn object is placed at a distance of 40 cm in front of a concave mirror of focal length 20 cm. The image produced is
View Solution
Knowledge Check
An object is placed at a distance of 20 cm from the pole of a concave mirror of focal length 10 cm. The distance of the image formed is
A+20cmB+10CmC−20cmD−10cmAn object is placed at a distance of 40 cm in front of a concave mirror of focal length 20 cm the image produced is
Avirtual and invertedBreal and erectCreal, inverted and diminishedDreal, inverted and of the same size as the objectA square ABCD of side 1mm is kept at distance 15cm in front of the concave mirror as shown in Figure. The focal length of the mirror is 10cm. The length of the perimeter of its image will be
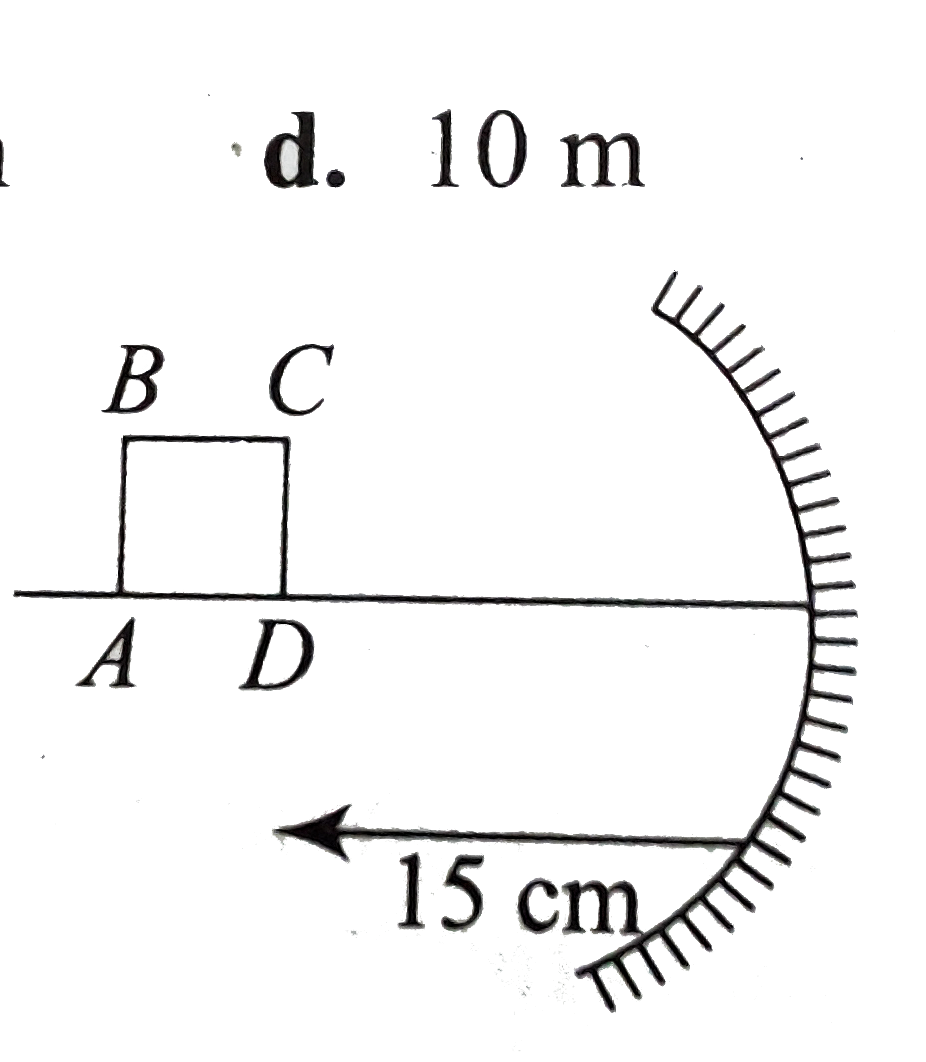 A8mmB2mmC12mmD6mm
A8mmB2mmC12mmD6mm
An object of size 10cm is placed at a distance of 50cm from a concave mirror of focal length 15cm. Calculate location, size and nature of the image.
View SolutionAn object is placed at a distance of 30 cm in front of a convex mirror of focal length 15 cm. Write four characteristics of the image formed by the mirror.
View SolutionAn object is kept at a distance 20 cm from a convex mirror of focal length 20 cm. The image will form at
View SolutionAn object is placed at 15 cm in front of a concave mirror whose focal length is 10 cm. The image formed will be
View SolutionA point object is placed at distance of 30 cm in front of a convex mirror of Focal length 30 cm. The image will form at
View Solution
