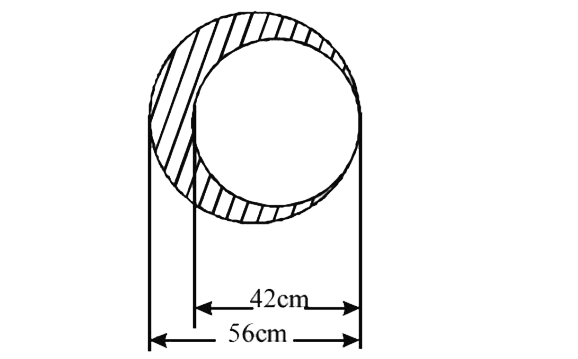
A circular plate of uniform thickness has a diameter of 56 cm . A circular portion of diameter 42 cm is removed from one edge of the plate as shown in the figure . Find the position of the centre of mass of the remaining portion .

Let r1 be the distance of the centre of the mass of remaining portion from centre of the bigger circle . Remaining area
A1=π[(56)2−(42)2]4
∴A1r1=A2r2 or r1=A2A1r1
or r1=π(42)2×4π[(56)2−(42)2]×4×71
or r1=42×42×798×14=9 cm
or r1=9 cm = Required distance C.M. of remaining part .
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS )
140 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - CHECK YOUR NEET VITALS
14 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
Similar Questions
A circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.
View SolutionA circular plate of uniform thickness has a diameter fo 56cm. A circular portion of diameter 42 cm is removed from one edge of the plate as shown in figure. Find the position of the centre of mass of the remaining portion.
View Solution
Knowledge Check
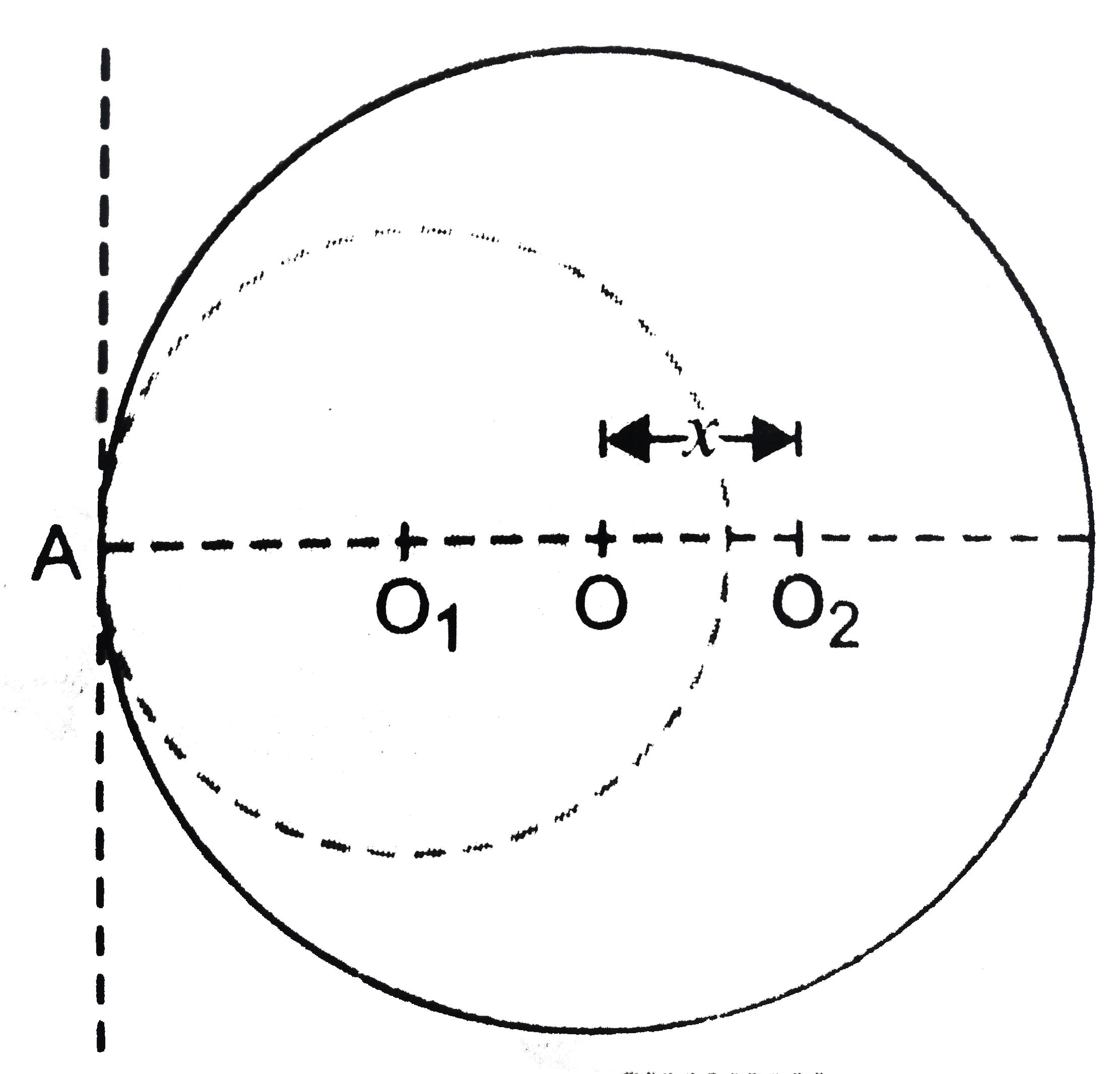
A circular plate of uniform thickness has a diameter of 28cm. A circular portion of diameter 21cm is removed from the plate as shown. Ois the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from 'O' by
 A5cmB9cmC4.5cmD5.5cm
A5cmB9cmC4.5cmD5.5cmA square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is
 Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above
Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above
A circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionA uniform circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from the edge of the plate. Find the position of the centre of mass of the remaining portion.
View SolutionA circular plate of uniform thickness has a diameter of 28cm. A circular portion of diameter 21cm is removed from the plate as shown. Ois the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from 'O' by

View SolutionA square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is

View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
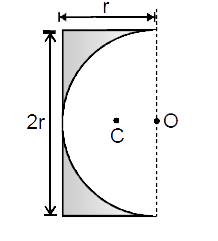
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is

View Solution
