A circular ring of radius R and mass m made of a uniform wire of cross sectional area A is rotated about a stationary vertical axis passing throgh its centre and perpendicular to the plane of the ring. If the breaking stress of the material of the ring is σb, then determine the maximum angular speed ωmax at which the ring may be rotated without failure.
To determine the maximum angular speed ωmax at which a circular ring of radius R and mass m can be rotated without failure, we can follow these steps:
Step 1: Understand the Forces Acting on the Ring
When the ring rotates, it experiences a centripetal force that is provided by the tension in the wire. The tension in the wire must counteract the centripetal force required to keep the mass of the ring moving in a circular path.
Step 2: Calculate the Centripetal Force
For a small segment of the ring, the mass dm can be expressed in terms of the total mass m and the angle dθ as follows:
dm=m2πdθ
The centripetal force Fc required for this mass to rotate at an angular speed ω is given by:
Fc=dm⋅R⋅ω2=m2πdθ⋅R⋅ω2
Step 3: Relate Tension to Centripetal Force
The tension T in the wire provides the necessary centripetal force. For the small segment dθ, the components of tension acting towards the center of the ring can be expressed as:
T⋅sin(dθ2)≈T⋅dθ2(for small angles)
Thus, the total centripetal force provided by the tension in the ring is:
Fc=2T⋅sin(dθ2)≈T⋅dθ
Step 4: Set Up the Equation
Equating the centripetal force to the tension components gives:
T⋅dθ=m2πdθ⋅R⋅ω2
Cancelling dθ from both sides (assuming dθ≠0):
T=mRω22π
Step 5: Relate Tension to Breaking Stress
The maximum tension Tmax that the material can withstand is given by the breaking stress σb multiplied by the cross-sectional area A:
Tmax=σb⋅A
Step 6: Set Maximum Tension Equal to Tension from Rotation
Setting the maximum tension equal to the expression derived from the centripetal force gives:
σb⋅A=mRω22π
Step 7: Solve for Maximum Angular Speed
Rearranging the equation to solve for ωmax:
ω2max=2πσbAmR
Taking the square root:
ωmax=√2πσbAmR
Final Answer
Thus, the maximum angular speed at which the ring may be rotated without failure is:
ωmax=√2πσbAmR
When the ring rotates, it experiences a centripetal force that is provided by the tension in the wire. The tension in the wire must counteract the centripetal force required to keep the mass of the ring moving in a circular path.
For a small segment of the ring, the mass dm can be expressed in terms of the total mass m and the angle dθ as follows:
dm=m2πdθ
The centripetal force Fc required for this mass to rotate at an angular speed ω is given by:
Fc=dm⋅R⋅ω2=m2πdθ⋅R⋅ω2
The tension T in the wire provides the necessary centripetal force. For the small segment dθ, the components of tension acting towards the center of the ring can be expressed as:
T⋅sin(dθ2)≈T⋅dθ2(for small angles)
Thus, the total centripetal force provided by the tension in the ring is:
Fc=2T⋅sin(dθ2)≈T⋅dθ
Equating the centripetal force to the tension components gives:
T⋅dθ=m2πdθ⋅R⋅ω2
Cancelling dθ from both sides (assuming dθ≠0):
T=mRω22π
The maximum tension Tmax that the material can withstand is given by the breaking stress σb multiplied by the cross-sectional area A:
Tmax=σb⋅A
Setting the maximum tension equal to the expression derived from the centripetal force gives:
σb⋅A=mRω22π
Rearranging the equation to solve for ωmax:
ω2max=2πσbAmR
Taking the square root:
ωmax=√2πσbAmR
Thus, the maximum angular speed at which the ring may be rotated without failure is:
ωmax=√2πσbAmR
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.2
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionA ring of radius r made of wire of density ρ is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring as shown in the figure. Determine the angular velocity (in rad/s) of ring at which the ring breaks. The wire breaks at tensile stress σ. Ignore gravity. Take σ/ρ=4 and r=1m.
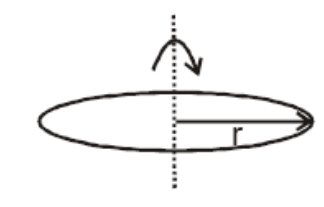
View SolutionA ring of radius r made of wire of density ρ is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring as shown in the figure. Determine the angular velocity (in rad/s) of ring at which the ring breaks. The wire breaks at tensile stress σ. Ignore gravity. Take σ/ρ=4 and r=1m.

View SolutionThe moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View SolutionA charge q is unifomly distrybuted over a nonconducting ring of radius R. The ring is rotated about an axis passing through its centre and perpendicular to the plane of the ring with frequency f. The ratio of electric potential to the magnetic field at the centre of the ring depends on.
View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View Solution
