A coil in the shape of an equilateral triangle of side l is suspended between the pole pieces of permanent magnet. Such that →B is in plane of the coil. If due to a current I in the triangle, a torque τ acts on it, the side l of the triangel is:
2(τ√3Bi)12
2√3(τBi)
2(τBi)12
1√3(τBi)
The correct Answer is:a
Torque acting on equilateral triangle in a magnetic field B is τ=iABsinθ
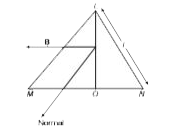
Area of triangle LMN,
A=√32l2andθ=90∘
Substituting the given values in expression for torque, we
get
τ=i×√34l2Bsin90∘
τ−√34il2B (∵sin90∘=1)
Here , l=2(τ√3Bi)12
Topper's Solved these Questions
Similar Questions
A coil in the shape of an equilateral triangle of side l is suspended between the pole pieces of a permanent magnet such that→B is in the plane of the coil. If due to a current i in the triangle a torque τ acts on it, the side l of the triangle is
View SolutionA coil in the shape of an equilateral triangle of side l is suspended between the pole pieces of a permanent magnet such that →B is in a plane of the coil. If due ot a current I, in the triangle a torque τ acts on it the side l of the triangle is given by N(τBiP)12. What will be the numerical value of N+P?
View Solution
Knowledge Check
A coil in the shape of an equilateral triangle of side l is suspended between the pole pieces of permanent magnet. Such that →B is in plane of the coil. If due to a current I in the triangle, a torque τ acts on it, the side l of the triangel is:
A2(τ√3Bi)12B2√3(τBi)C2(τBi)12D1√3(τBi)Choose the most appropriate option.
A coil in the shape of an equilateral triangle of side l is suspended between two pole pieces of a permanent magnet, such that magnetic eld, B is in plane of the coil. If due to a current I in the triangle, a torque τ acts on it, the side I of the triangle isA2(t√3Bl)12B2√3(τBl)C2(τBl)12D1√3τBlA coil in the shape of an equilateral triangle of side I suspended between the pole pieces of a permanent magnet such that is in plane of the coil. If due to current I in the triangle a torque z acts on it, the side I of the triangle is
A2/sqrt3(tau/"BI")^"1/2"B23(τBI)C2(tau/(sqrt3BI))^(1//2)D1√3τBI
A coil in the shape of an equilateral triangle of side 10 cm lies in a vertical plane between the pole pieces of permanent magnet producing a horizontal magnetic field 20 mT. The torque acting on the coil when a current of 0.2 A is passed through it and its plane becomes parallel to the magnetic field will be √x×10−5Nm . The value of x is ____
View SolutionA coil in the shape of an equilateral triangle of side 0.01 m is suspended from the vertex such that is hanging in a vertical plane between pole pieces of a permanent magnet producing a horizontal magnetic field of (4×10−2T).If a current of 1A is passing through it and the magnetic field is parallel to its field,then the torque acting on the coil is
View SolutionA coil in the shape of an equilateral triangle of side 0.01m is suspended from the vertex such that it is hanging in a vertical plane between pole pieces of a permanent magnet producing a horizontal magnetic field of 4×10−2 T. If a current of 1A is passing through it and the magnetic field is parallel the magnetic field is parallel to its plane, then the torque acting on the coil is
View SolutionA coil in the shape of an equilateral triangle of side 0.02 m is suspended from a vertex such that it is hanging in a vertical plane between the pole pieces of a permanent magnet producing a horizontal magnetic field of 5×10−2T. Find the couple acting on the coil when a current of 0.1 A is passed through it and the magnetic field is parallel to its plane.
View SolutionA loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.

View Solution
