A coil of 100 turns and 1cm radius is kept coaxially within a long solenoid of 8 turns per cm and 5 cm radius. Find the mutual inductance.
To find the mutual inductance between a coil and a solenoid, we can use the formula for mutual inductance M:
M=N1⋅Φ21I2
Where:
- N1 is the number of turns in the coil,
- Φ21 is the magnetic flux through one turn of the coil due to the solenoid,
- I2 is the current in the solenoid.
Step 1: Calculate the magnetic field inside the solenoid
The magnetic field B inside a long solenoid is given by the formula:
B=μ0nI
Where:
- μ0=4π×10−7T m/A (permeability of free space),
- n is the number of turns per unit length of the solenoid,
- I is the current flowing through the solenoid.
Given that the solenoid has 8 turns per cm, we convert this to turns per meter:
n=8turns/cm=800turns/m
Step 2: Calculate the magnetic flux through the coil
The area A of the coil can be calculated using the formula for the area of a circle:
A=πr2
Where r is the radius of the coil. Given that the radius of the coil is 1 cm (0.01 m):
A=π(0.01)2=π×0.0001m2=3.14×10−4m2
The magnetic flux Φ through one turn of the coil is given by:
Φ=B⋅A
Substituting the expression for B:
Φ=(μ0nI)⋅A=(4π×10−7)⋅(800)⋅(3.14×10−4)
Step 3: Calculate the mutual inductance
Now, substituting Φ into the mutual inductance formula:
M=N1⋅Φ21
Where N1=100 (number of turns in the coil). Thus:
M=100⋅Φ
Final Calculation
Now we can calculate M using the values obtained.
1. Calculate B:
- B=μ0nI=(4π×10−7)⋅(800)
2. Calculate A:
- A=3.14×10−4m2
3. Calculate Φ:
- Φ=B⋅A
4. Finally, calculate M:
- M=100⋅Φ
- N1 is the number of turns in the coil,
- Φ21 is the magnetic flux through one turn of the coil due to the solenoid,
- I2 is the current in the solenoid.
- μ0=4π×10−7T m/A (permeability of free space),
- n is the number of turns per unit length of the solenoid,
- I is the current flowing through the solenoid.
- B=μ0nI=(4π×10−7)⋅(800)
- A=3.14×10−4m2
- Φ=B⋅A
- M=100⋅Φ
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Illustration
25 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Practice Exercise 5.1
12 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
389 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
Similar Questions
A circular coil P of 100 turns and radius 2cm is placed coaxially at the centre of another circular coil Q of 100 turns and radius 20cm . Calculate (a) the mutual inductance of the coils
(b) the induced emf in coil P when the current in the coil Q decreases from 5A to 3A in 0.04 sec (Take π2=10)
View SolutionA conducting wire of 100 turns is wound over and near the centre of a solenoid of 100 cm length and 2 cm radius having 600 turns. Calculate mutual inductance of two coils.
View Solution
Knowledge Check
A srot soleniod of radius a, number of turns per unit length n2, and length L is kept coaxially inside a very long solenoid of radius b, number of turns per unit length n2. What is the mutual inductance of the system?
Aμ0πb2n1n2LBμ0πa2n1n2L2Cμ0πa2n1n2LDμ0πb2n1n2L2A solenoid having 500 turns and length 2 m has radius of 2 cm , the self inductance of solenoid
A4×10−4HB2×10−4HC8×10−4HD16×10−4H
A coil with 1500 turns, a radius of 5.0 cm and a resistance of 12Ω surrounds a solenoid with 240turns/cm and a radius of 4 cm , see figure. The current in the solenoid changes at a constant rate from 0 to 20 A in 0.10 s. Calculate the magnitude of the induced current (in mA) in the 1500 turn coil (π2=10 Neglect self inductance of the coil).
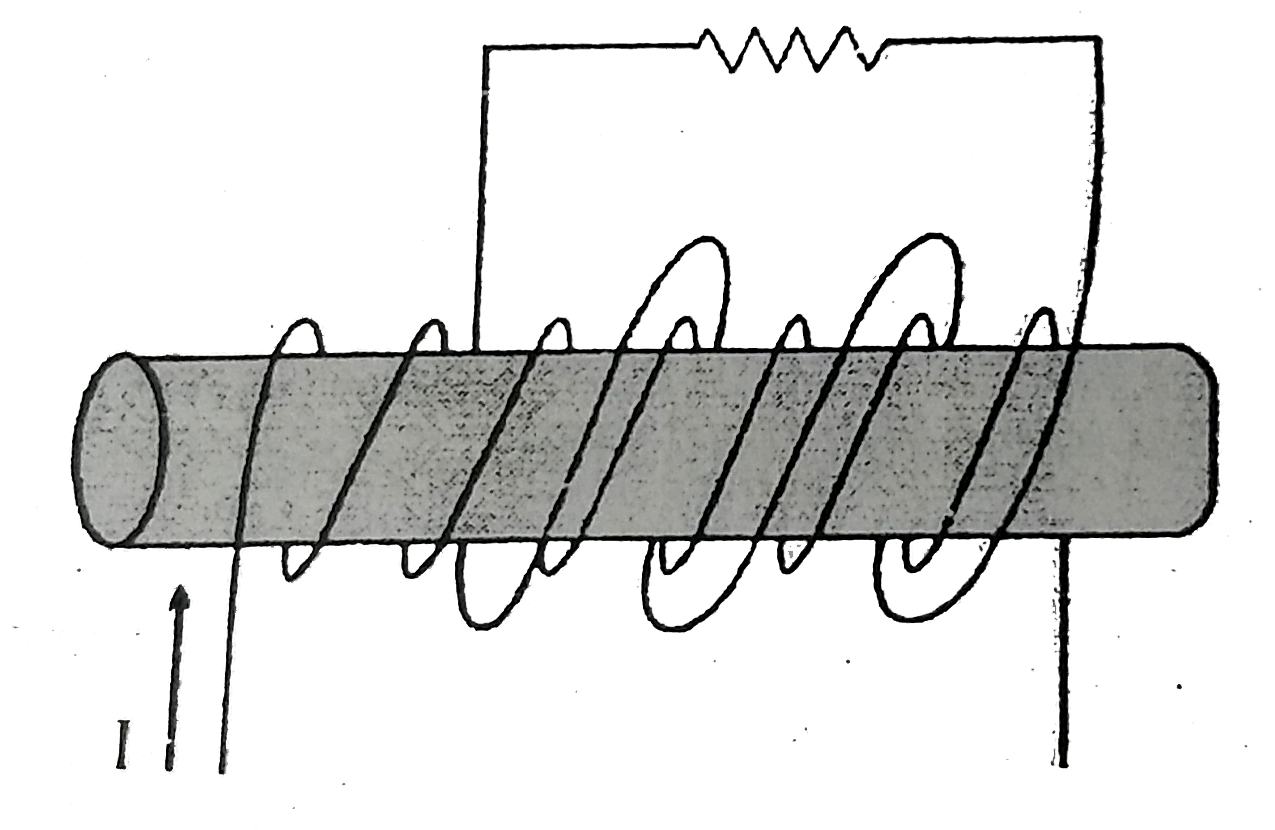
View SolutionIn Fig. 30-54, a 120-turn coil of radius 1.8 cm and resistance 5.3 Ω is coaxial with a solenoid of 220 turns/cm and diameter 3.2 cm. The solenoid current drops from 0.42 A to zero in time interval Δt=0.67 s. What current is induced in the coil during Δt?
View SolutionA solenoid coil of 300turns/m is carrying a current of 5A. The length of the solenoid is 0⋅5m and has a radius of 1cm. Find the magnitude of the magnetic field well inside the solenoid.
View SolutionTwo solenoids A and B having radius of 5 cm and 3 cm respectively are placed coaxially such that A surrounds B. The length of both the solenoid is 30 cm and number of turns of A and B are 70 turns per cm and 50 turns per cm, respectively. What will be the mutual inductance of the system?
View SolutionFind the length of a solenoid of radius 2 cm and 800 turns per metre having self-inductance of 0.115 H.
View SolutionA solenoid of length 20cm, area of cross- section 4.0cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross - sectional area 8.0cm ^2 and length 10 cm. Find the mutual inductance between the solenoids.
View Solution
