A coil with inductance and active resistance is connected in series with an inductance free resistance . An alternating voltage with effective value and frequency is applied across the terminals of this circuit. At what value of the resistance will the maximum heat power be generated in the circuit ? What is it equal to ?
Power in the circuit
For P to be maximum
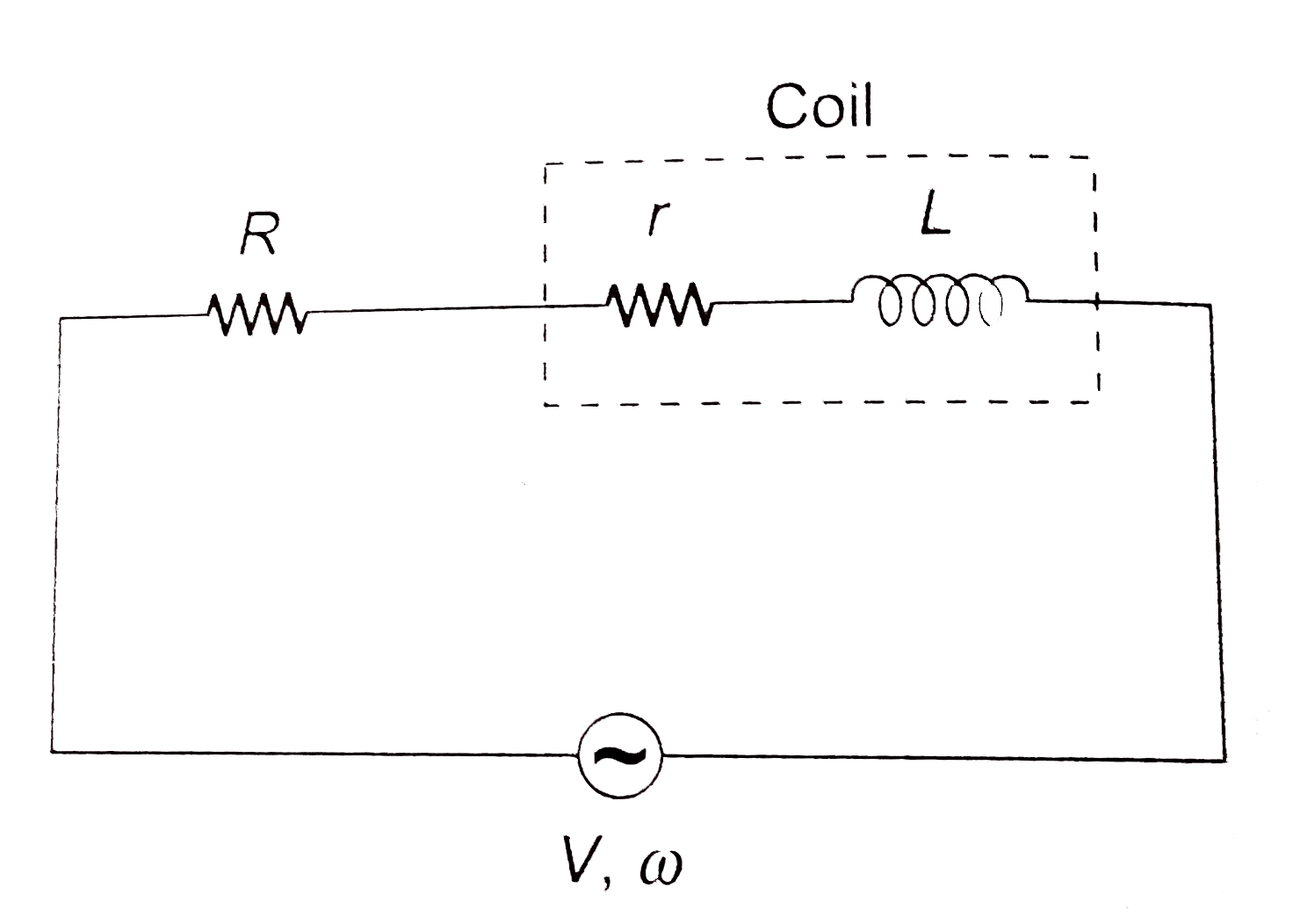 .
.
Topper's Solved these Questions
Similar Questions
A coil with inductance L=0.70H and active resistance r=20Ω is connected in series with an inductance − free resistance R. An alternating voltage with effective value V=220V and frequency ω=314s−1 is a applied across the terminals of this circuit. At what value of the resistance R will the maximum heat power be generated in the circuit ? What is it equal to ?
View SolutionA solenoid with inductance L=7mH and active resistance R=44Ω is first connected to a source of direct voltabe V0 and then to a source of sinusoidal voltage with effective value V=V0 . At what frequency of the oscillator will be power consumed by the solenoid be η=5.0 times less than in the former case ?
View Solution
Knowledge Check
In an AC circuit, a resistance R is connected in series with an inductance L. If the phase angle between the voltage and the current is pi//4 then the value of ihe inductive reactance is
AR/4BR/2CRDR/sAn alternating supply of 220 V is applied across a circuit with resistance 22Ω and impedance 44Ω. The power dissipated in the circuit is
A1100 WB550 WC2200 WD(2200/3) WAn inductance L and capacitance C and resistance R are connected in series across an AC source of angular frequency ω. If ω2>1LC then
Aemf leads the currentBboth the emf and the current are in phaseCcurrent lead the emfDemf lags behind the current
A series circuit consisting of a capacitor with capacitance C=22μF and a coil with active resistance R=20Ω and iniductance L=0.35H is connected to a source of alternating voltage with amplitude Vm=180V and frequency ω=314s−1. Find :
(a) the current amplitude in the circuit,
(b) the phase difference between the current and the external voltage ,
(c) the amplitudes of voltage across the capacitor and the coil.
View SolutionIn the given circuit if the internal resistance of the batteries are negligible, then for what value of resistance R(inΩ) will the thermal power generated in it be maximum.

View SolutionIn an L-R circuit, an inductance of 0.1 H and a resistance of 1Ω are connected in series with an ac source of voltage V = 5 sin 10 t. The phase difference between the current and applied voltage will be
View SolutionIn an L-R circuit, an inductance of 0.1 H and a resistance of 1Ω are connected in series with an ac source of voltage V = 5 sin 10 t. The phase difference between the current and applied voltage will be
View SolutionA 100V voltmeter having an internal resistance of 20kΩ is connected in series with a large resistance R across a 110V line. What is the magnitude of resistance R if the voltmeter reads 5V?
View Solution
