A concave mirror has a focal length of 10 cm. Where can we place the object so that the image formed is magnified to twice the size of object ?
To solve the problem step by step, we will use the mirror formula and the magnification formula.
Step 1: Understand the given data
We have a concave mirror with a focal length f=−10 cm (negative because it is a concave mirror). We need to find the object distance u such that the image formed is magnified to twice the size of the object.
Step 2: Write the magnification formula
The magnification M is given by the formula:
M=hiho=−vu
where:
- hi is the height of the image,
- ho is the height of the object,
- v is the image distance,
- u is the object distance.
Given that the image is twice the size of the object, we have:
M=2
Thus, we can write:
2=−vu
From this, we can express v in terms of u:
v=−2u
Step 3: Use the mirror formula
The mirror formula is given by:
1f=1v+1u
Substituting the focal length f=−10 cm and v=−2u:
1−10=1−2u+1u
Step 4: Simplify the equation
Rearranging the equation:
1−10=−12u+1u
Finding a common denominator for the right side:
1−10=−12u+22u=12u
Now we have:
1−10=12u
Step 5: Cross-multiply to solve for u
Cross-multiplying gives:
2u=−10
Thus:
u=−5 cm
Step 6: Conclusion
The object should be placed at a distance of 5 cm in front of the mirror (the negative sign indicates the direction towards the mirror).
Final Answer:
The object should be placed at 5 cm in front of the concave mirror.
---
We have a concave mirror with a focal length f=−10 cm (negative because it is a concave mirror). We need to find the object distance u such that the image formed is magnified to twice the size of the object.
The magnification M is given by the formula:
M=hiho=−vu
where:
- hi is the height of the image,
- ho is the height of the object,
- v is the image distance,
- u is the object distance.
M=2
Thus, we can write:
2=−vu
From this, we can express v in terms of u:
v=−2u
The mirror formula is given by:
1f=1v+1u
Substituting the focal length f=−10 cm and v=−2u:
1−10=1−2u+1u
Rearranging the equation:
1−10=−12u+1u
Finding a common denominator for the right side:
1−10=−12u+22u=12u
Now we have:
1−10=12u
Cross-multiplying gives:
2u=−10
Thus:
u=−5 cm
The object should be placed at a distance of 5 cm in front of the mirror (the negative sign indicates the direction towards the mirror).
The object should be placed at 5 cm in front of the concave mirror.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (2)
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (3)
18 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A converging lens has a focal length of 15 cm. Determine the position where an object can be placed so that the image obtained is twice the size of object.
View SolutionA concave mirror has a focal length of 5 cm. When an object is placed at a distance of 15 cm from the mirror, then the image is formed in front of the mirror at ____cm.
View Solution
Knowledge Check
A concave mirror has focal length 15 cm. Where should an object be placed in front of the mirror so that the image formed is three times the size of the object?
(i) 7.5 cm
(ii) 10 cm
(iii) 17.5 cm
(iv) 20 cmA(i),(ii)B(ii),(iii)C(ii),(iv)D(i),(iii)A concave mirror has a focal length 20 cm. The distance between the two positions of the object for which the image size is double of the object size is
A20 cmB40 cmC30 cmD60 cmA concave mirror has a focal length of 10 cm. Where can we place the object so that the image formed is magnified to twice the size of object ?
A12cmB25cmC8cmD15cm
A concave mirror has a focal length of 20 cm. Find the position or positions of an object for which the image-size is double of the object-size.
View SolutionA concave morror has a focal lengh of 10 cm. Wherer should and object be placed in front of this concave mirror so as too obtain an image which is real, inverted and same size as the object ?
View SolutionA plane mirror is placed 22.5 cm in front of a concave mirror of focal length 10 cm. Find where an object can be placed between the two mirrors, so that the first image in both the mirrors by concave mirror.Also find out magnification of the image produced by concave mirror
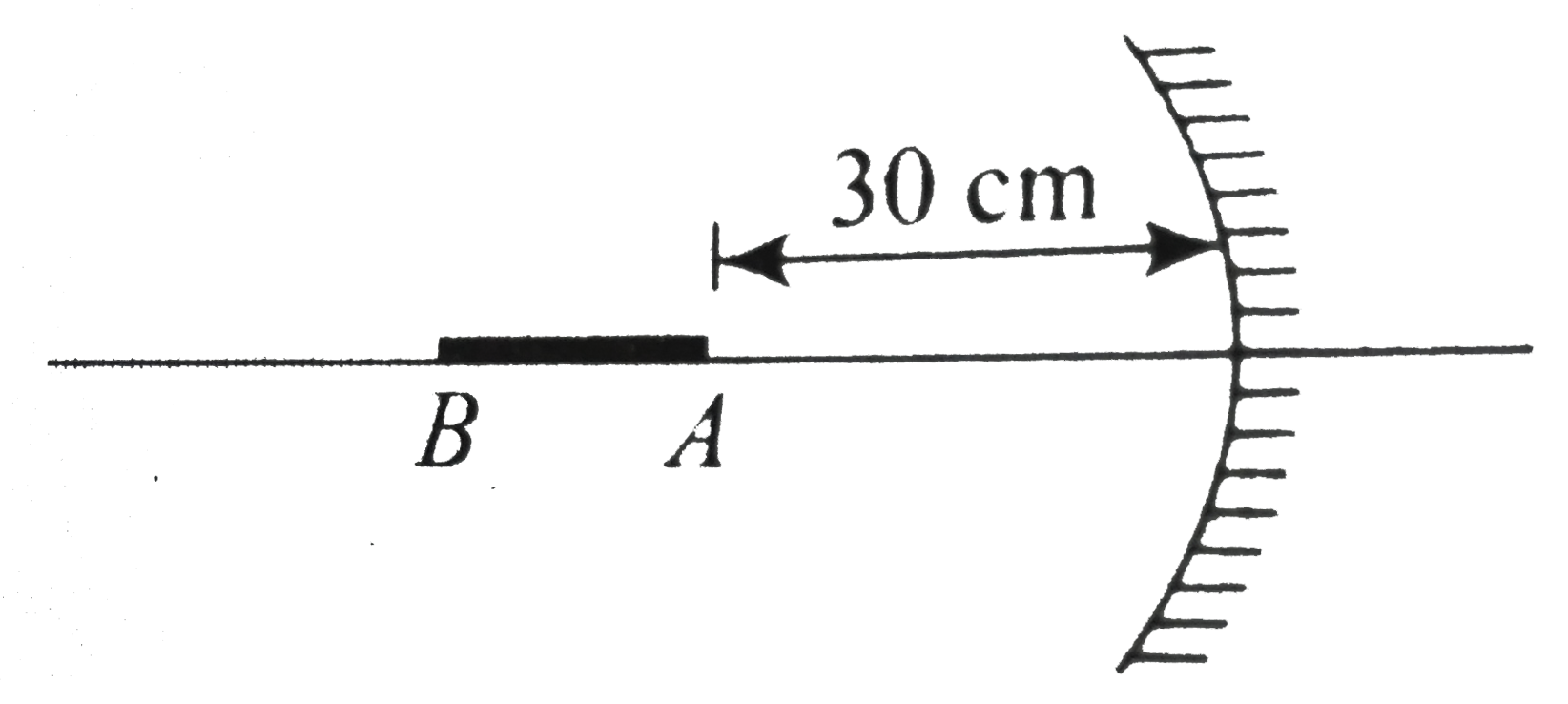
View SolutionObject AB is placed on the axis of a concave mirror of focal length 10cm. End A of the object is at 30cm from the mirror. Find the length of the image
a. if length of object is 5cm.
b. if length of object is 1 mm.
View SolutionA concave mirror of focal length 8 cm forms an inverted image of an object placed at a certain distance. If the image is twice as large as object, where is the image formed ?
View Solution
