A concave mirrorr of focal length is placed at a distance of from a convex lens of focal length . A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance must equal.
The correct Answer is:C
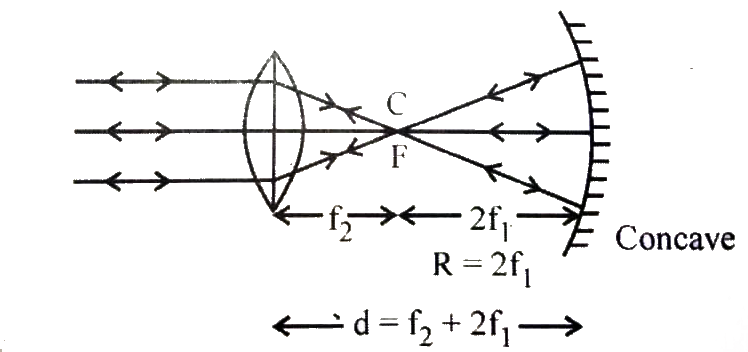
The parallel beam of light is focused at the focus F of the convex lens. If F coincides with the centre of curvature C of the concave mirror, then the rays reflected from the mirror will again come to C and the rays from F, will become parallel after passing through the lens.
Distance
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)EXERCISE - TEST YOUR GRASP10videos
RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)
- BOOK - MARVEL PUBLICATIONCHAPTER - MEASUREMENTS EXERCISE - TEST YOUR GRASP10videos
MEASUREMENTS
- BOOK - MARVEL PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - Test Your Grasp10videos
REFRACTION OF LIGHT
Similar Questions
Knowledge Check
- Question 1 - Select One
An object is situated at a distance off/2from a convex lens of focal lengthfDistance of image will be-
A+(f/2)B+(f/3)C+(f/4)D−f - Question 2 - Select One
A concave lens of focal length 20 cm placed in contact with ah plane mirror acts as a convex mirror of focal length
A10 cmB40 cmC60 cmD20 cm - Question 3 - Select One
A convex lens of focal length 'f' is placed in contact with a concave lens of the same focal length. The equivalent focal length of the combination is
AfBinfinityCf2Dzero
A convex lens of focal length 10 cm is placed in contact with a concave lens of focal length 20 cm. The focal length of this combination of lenses will be:
View SolutionA convex lens of focal length 20 cm is placed in contact with a concave lens of focal length 10 cm. What is the focal length and power of the combination ?
View SolutionA convex mirror has a focal length f. A real object is placed at a distance f in front of it from the pole produces an image at
View SolutionA convex lens of focal length 40cm is in contact with a concave lens of focal length 25cm. The power of the combination is
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View Solution

