A concrete sphere of radius R has cavity of radius r which is packed with sawdust. The specific gravities of concrete and sawdust are respectively 2.4and0.3 for this sphere to float with its entire volume submerged under water. Ratio of mass of concrete to mass of swadust will be
8
4
3
Zero
The correct Answer is:B
To solve the problem, we need to find the ratio of the mass of concrete to the mass of sawdust in a concrete sphere with a cavity filled with sawdust, given that the sphere floats with its entire volume submerged in water.
1. Understanding the Problem:
- We have a concrete sphere of radius R with a cavity of radius r filled with sawdust.
- The specific gravities of concrete and sawdust are given as 2.4 and 0.3 respectively.
- We need to find the ratio of the mass of concrete to the mass of sawdust.
2. Calculate the Volume of Concrete and Sawdust:
- The volume of the entire sphere (concrete + cavity) is:
Vtotal=43πR3
- The volume of the cavity (sawdust) is:
Vcavity=43πr3
- The volume of concrete is:
Vconcrete=Vtotal−Vcavity=43πR3−43πr3=43π(R3−r3)
3. Calculate the Mass of Concrete and Sawdust:
- The density of concrete (ρc) and sawdust (ρs) can be calculated using their specific gravities:
ρc=2.4×ρwaterandρs=0.3×ρwater
- The mass of concrete (mc) is:
mc=Vconcrete×ρc=43π(R3−r3)×(2.4×ρwater)
- The mass of sawdust (ms) is:
ms=Vcavity×ρs=43πr3×(0.3×ρwater)
4. Finding the Ratio of Mass of Concrete to Mass of Sawdust:
- The ratio of the mass of concrete to the mass of sawdust is given by:
mcms=43π(R3−r3)×(2.4×ρwater)43πr3×(0.3×ρwater)
- Simplifying this expression:
mcms=(R3−r3)×2.4r3×0.3
- Further simplifying gives:
mcms=2.40.3×R3−r3r3=8×R3−r3r3
5. Final Expression:
- Thus, the ratio of the mass of concrete to the mass of sawdust is:
mcms=8×R3−r3r3
- We have a concrete sphere of radius R with a cavity of radius r filled with sawdust.
- The specific gravities of concrete and sawdust are given as 2.4 and 0.3 respectively.
- We need to find the ratio of the mass of concrete to the mass of sawdust.
- The volume of the entire sphere (concrete + cavity) is:
Vtotal=43πR3
- The volume of the cavity (sawdust) is:
Vcavity=43πr3
- The volume of concrete is:
Vconcrete=Vtotal−Vcavity=43πR3−43πr3=43π(R3−r3)
- The density of concrete (ρc) and sawdust (ρs) can be calculated using their specific gravities:
ρc=2.4×ρwaterandρs=0.3×ρwater
- The mass of concrete (mc) is:
mc=Vconcrete×ρc=43π(R3−r3)×(2.4×ρwater)
- The mass of sawdust (ms) is:
ms=Vcavity×ρs=43πr3×(0.3×ρwater)
- The ratio of the mass of concrete to the mass of sawdust is given by:
mcms=43π(R3−r3)×(2.4×ρwater)43πr3×(0.3×ρwater)
- Simplifying this expression:
mcms=(R3−r3)×2.4r3×0.3
- Further simplifying gives:
mcms=2.40.3×R3−r3r3=8×R3−r3r3
- Thus, the ratio of the mass of concrete to the mass of sawdust is:
mcms=8×R3−r3r3
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Assertion Reasoning15videos
FLUID MECHANICS
- BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - NEET Questions7videos
FLUID MECHANICS
- BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Application Of Bernoulli'S Theorem And Velocity Of Efflux19videos
FLUID MECHANICS
- BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test30videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
Similar Questions
A concrete sphere of radius R has cavity of radius r which is packed with sawdust. The specific gravities of concrete and sawdust are respectively 2.4and0.3 for this sphere to float with its entire volume submerged under water. Ratio of mass of concrete to mass of swadust will be
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Inside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
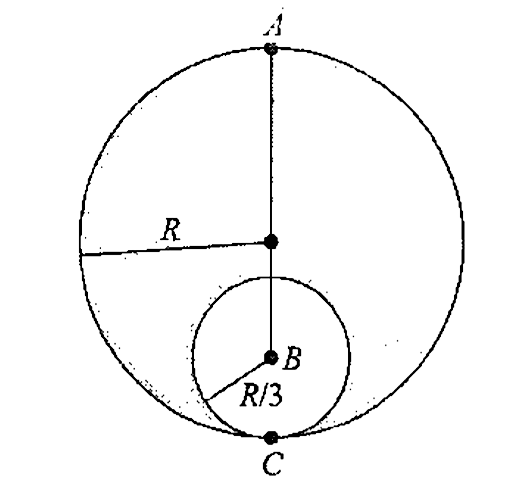 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only - Question 2 - Select One
If the radius of a sphere is 2r , them its volume will be
A43πr3B4πr3C8πr33D323πr3 - Question 3 - Select One
A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
 A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1
A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1
A non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
View SolutionThe ratio of masses of a cubical block of wood and a chunk of concrete is 3/5 so that the combination just floats with entire volume submerged under water. If the specific gravity of wood is 0.5 then specific gravity of concrete will be
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
If q1 is shifted to the centre of the cavity, then: (choose the correct alternative)View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric potential at the centre of the cavity will be :View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric field (magnitude only) at the center of the cavity will be :View Solution

