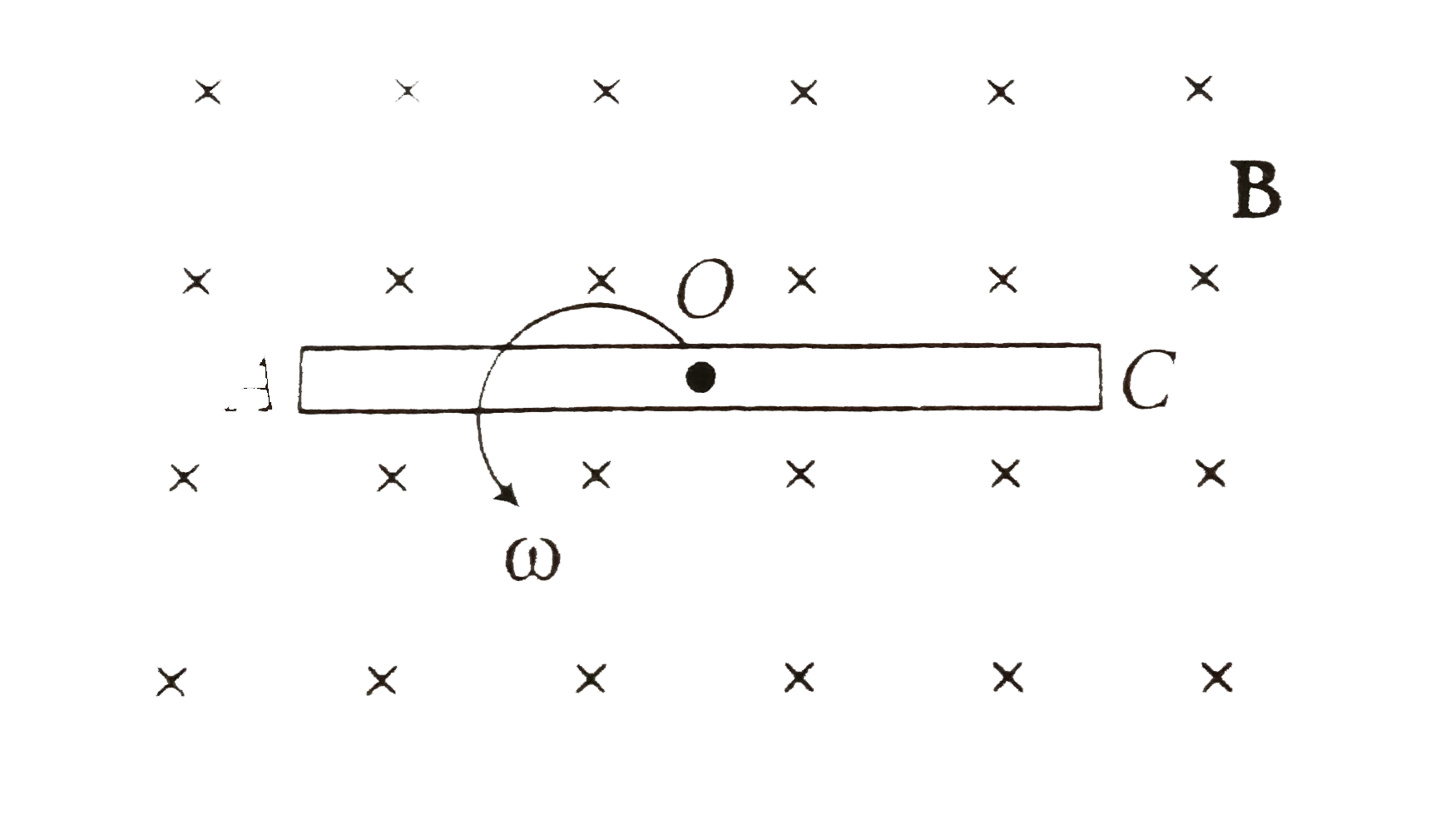
A conducting rod of length is rotated about point in a uniform magnetic field directed into the plane of the paper. . Find .

The correct Answer is:C
For rotating rod, induced emf,
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionRod PQ of length 2l is rotating about its midpoint C in a uniform magnetic field B which is perpendicular to the plane of rotation of the rod . Find the induced emf between PQ and PC. Draw the circuit diagram of parts PC and CQ.

View Solution
Knowledge Check
A conducting rod AC of length 4l is rotated about point O in a uniform magnetic field →B directed into the plane of the paper. AO=landOC=3l. Find VA−VC.
 AVA−Vo=Bωl22BVo−VC=72Bωl2CVA−Vc=4Bωl2DVc−Vo=92Bωl2
AVA−Vo=Bωl22BVo−VC=72Bωl2CVA−Vc=4Bωl2DVc−Vo=92Bωl2A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __
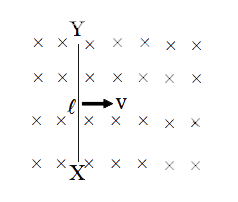 AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating
AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heatingA conducting rod AB moves parallel to x-axis in a uniform magnetic field pointing perpendicular and into the plane of paper. The end A of the rod
 Agets positively chargedBgets negatively chargedCremains neutralDgets positively charged first and then negatively charged
Agets positively chargedBgets negatively chargedCremains neutralDgets positively charged first and then negatively charged
A copper rod of length l rotates an angular velocity ω in a uniform magnetic field B as show in figure . What is the induced emf across its ends ?
View SolutionRod PQ of length 2l is rotating about one end P in a uniform magnetic field B which is perpendicular to the plane of rotation of the rod . Point M is the mid- point of the rod. Find the induced emf between M and Q if the potential between P and Q is 100V.

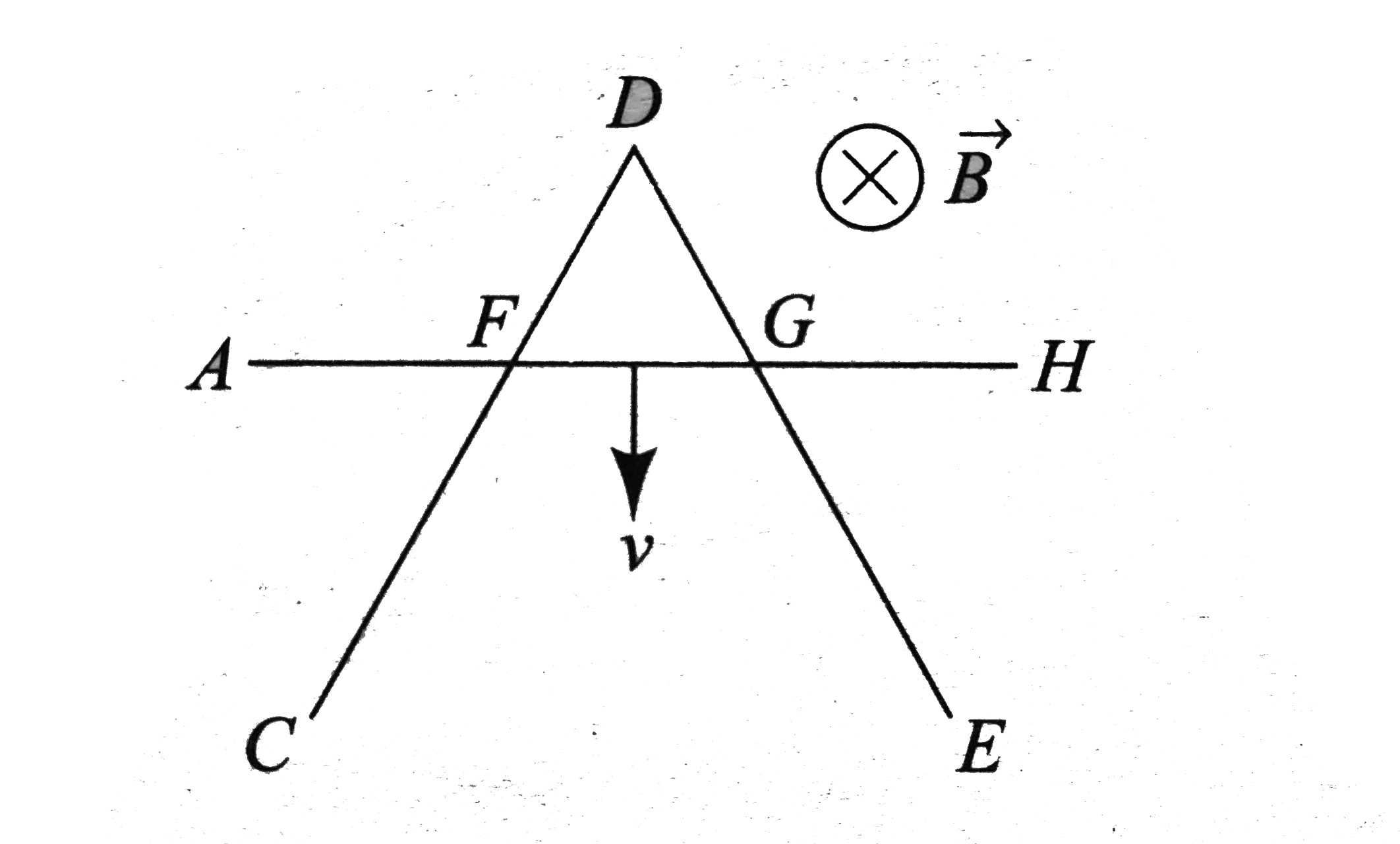
View SolutionA long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then
View SolutionA conducting rod PQ of length L=1.0m is moving with a uniform speed v=2.0ms−1 in a uniform magnetic field B=4.0T directed into the plane of the paper.
A capacitor of capacity C=10μF is connected as shown in , then

View SolutionA conducting rod PQ of length l=1.0m is moving with a uniform speed v2.0m/s in a uniform magnetic field B=4.0T directed into the paper.
A capacitor of capacity C=10μF is connected as shown in figure. Then
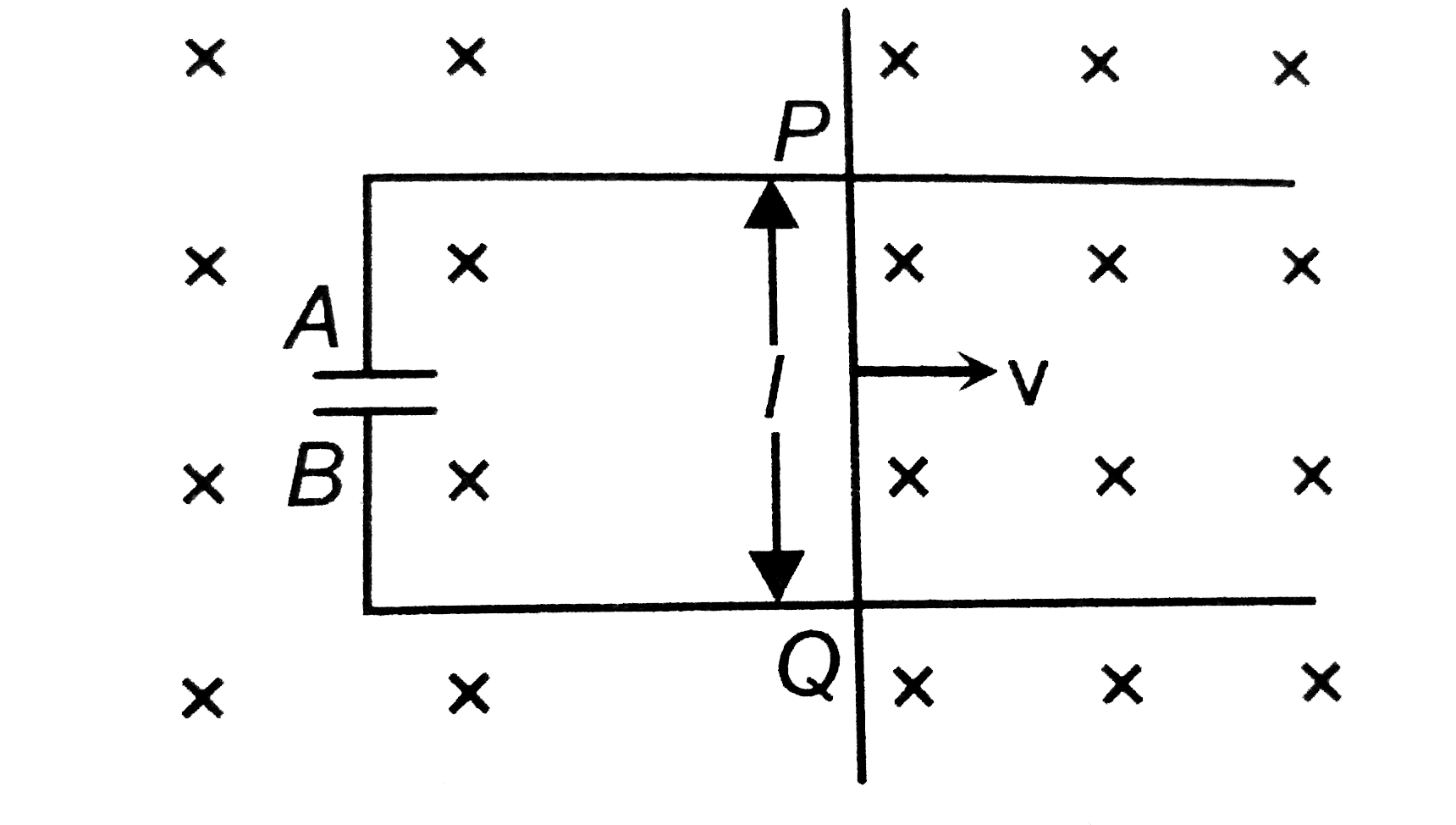
View Solution
