A conducting sphere S1 of radius r is attached to an insulating handle. Another conduction sphere S2 of radius R is mounted on an insulating stand. S2 is initially uncharged. S1 is given a charge Q brought into contact with S2 and removed. S1 is recharge such that the charge on it is again Q and it is again brought into contact with S2 and removed. This procedure is repeated n times.
a. Find the electrostatic energy of S2 after n such contacts with S1.
b. What is the limiting value of this energy as n→∞ ?
To solve the problem step by step, we will analyze the situation involving two conducting spheres, S1 and S2, and determine the electrostatic energy of S2 after n contacts with S1, as well as the limiting value of this energy as n approaches infinity.
Step 1: Understanding the Charge Transfer Process
When the charged sphere S1 (with charge Q) comes into contact with the uncharged sphere S2, charge will redistribute between the two spheres until they reach the same potential.
1. Initial Charges:
- Charge on S1: Q
- Charge on S2: 0
2. Final Charges after First Contact:
- Let Q1 be the charge transferred from S1 to S2.
- The potential of S1 after losing charge Q1 is given by:
V1=K(Q−Q1)r
- The potential of S2 after gaining charge Q1 is:
V2=KQ1R
- Setting V1=V2:
K(Q−Q1)r=KQ1R
Step 2: Solving for Charge Transferred Q1
From the equality of potentials, we can simplify:
(Q−Q1)R=Q1r
QR−Q1R=Q1r
QR=Q1(R+r)
Q1=QRR+r
Step 3: Charge on S2 after the First Contact
After the first contact, the charge on S2 becomes:
Q1=QRR+r
Step 4: Repeating the Process
After the first contact, S1 is recharged to Q and the process is repeated. The charge transferred during the second contact Q2 can be calculated similarly:
Q2=Q(R+r)R+r+r=Q(R+r)R+2r
Continuing this process, we can generalize the charge transferred after n contacts:
Qn=QRR+r(1−(rR+r)n)
Step 5: Electrostatic Energy of S2
The electrostatic energy Un of S2 after n contacts is given by:
Un=12Q2nC
Where C is the capacitance of S2:
C=4πϵ0R
Substituting Qn:
Un=12⋅14πϵ0R(QRR+r(1−(rR+r)n))2
Step 6: Limiting Value as n→∞
As n→∞:
U∞=12⋅14πϵ0R(QRR+r)2
Final Result
Thus, the electrostatic energy of S2 after n contacts is:
Un=Q2R2(R+r)2(4πϵ0)
And the limiting value of this energy as n→∞ is:
U∞=Q28πϵ0R
When the charged sphere S1 (with charge Q) comes into contact with the uncharged sphere S2, charge will redistribute between the two spheres until they reach the same potential.
- Charge on S1: Q
- Charge on S2: 0
- Let Q1 be the charge transferred from S1 to S2.
- The potential of S1 after losing charge Q1 is given by:
V1=K(Q−Q1)r
- The potential of S2 after gaining charge Q1 is:
V2=KQ1R
- Setting V1=V2:
K(Q−Q1)r=KQ1R
From the equality of potentials, we can simplify:
(Q−Q1)R=Q1r
QR−Q1R=Q1r
QR=Q1(R+r)
Q1=QRR+r
After the first contact, the charge on S2 becomes:
Q1=QRR+r
After the first contact, S1 is recharged to Q and the process is repeated. The charge transferred during the second contact Q2 can be calculated similarly:
Q2=Q(R+r)R+r+r=Q(R+r)R+2r
Qn=QRR+r(1−(rR+r)n)
The electrostatic energy Un of S2 after n contacts is given by:
Un=12Q2nC
Where C is the capacitance of S2:
C=4πϵ0R
Substituting Qn:
Un=12⋅14πϵ0R(QRR+r(1−(rR+r)n))2
As n→∞:
U∞=12⋅14πϵ0R(QRR+r)2
Thus, the electrostatic energy of S2 after n contacts is:
Un=Q2R2(R+r)2(4πϵ0)
And the limiting value of this energy as n→∞ is:
U∞=Q28πϵ0R
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
155 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Match the refining methods (Column I) with (Column II).
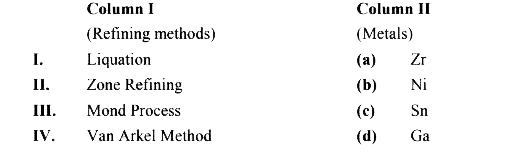
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionSelf energy of conducting sphere of radius .r. carrying charge .Q. is ______
View SolutionA sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ratio of electric flux through S1andS2,
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final charge on initially neutral conducting sphere is :
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View SolutionA solid insulating sphere of radius R is given a charge Q. If at a point inside the sphere the potential is 1.5 times the potential at the surface, this point will be
View SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2. Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionTwo metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
View Solution
