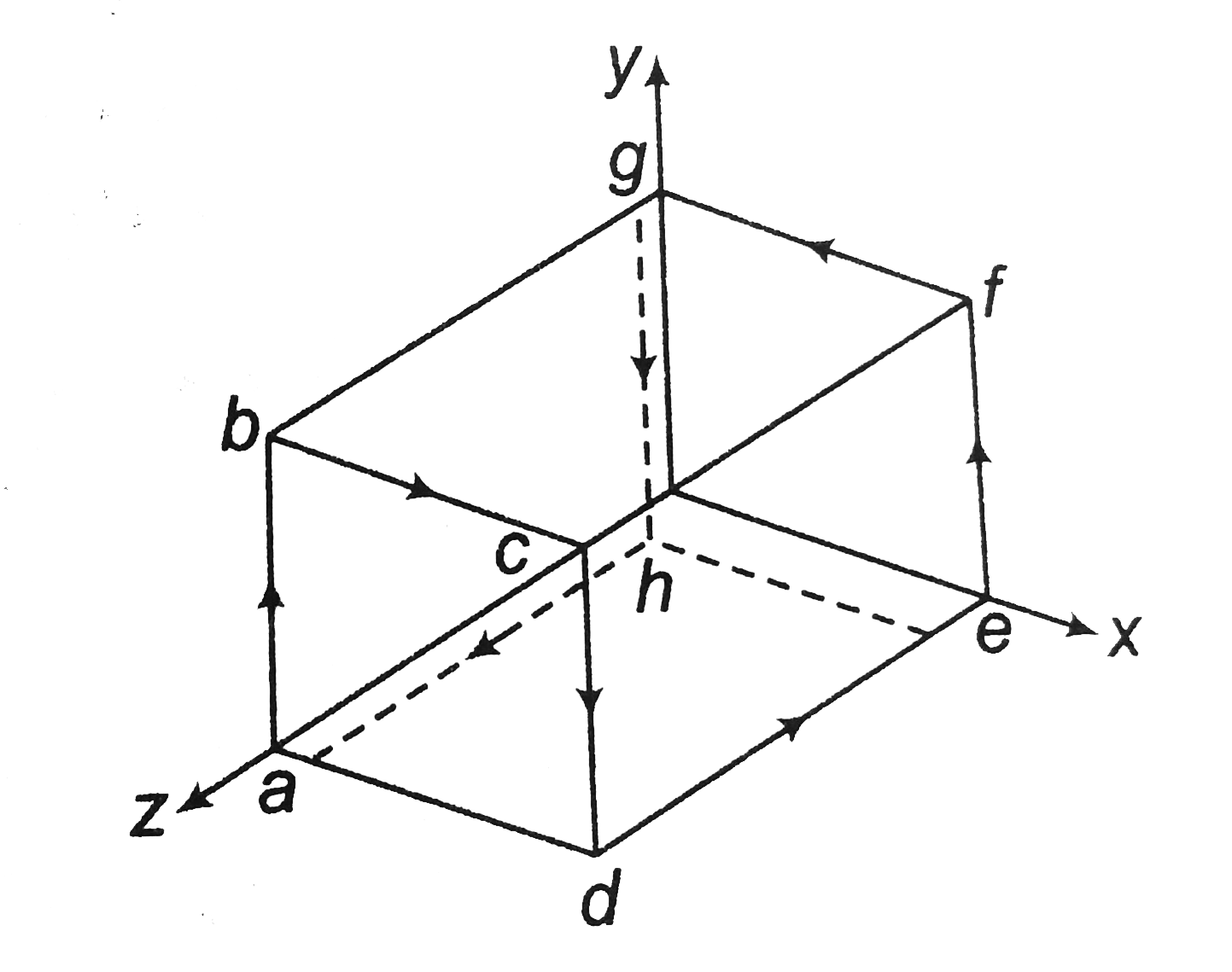
A conductor carries a constant current I along the closed path abcdefgha involving 8 of the 12 edges of length l. Find the magnetic dipole moment of the closed path.
To find the magnetic dipole moment of the closed path abcdefgha, we can follow these steps:
Step 1: Identify the Closed Path and Its Faces
The closed path abcdefgha consists of 8 edges of length l. We can divide this path into three distinct faces:
1. Face 1: BCFG
2. Face 2: CFEG
3. Face 3: BGHA
Step 2: Calculate the Magnetic Moment for Each Face
The magnetic dipole moment M for a current-carrying loop is given by the formula:
M=I⋅A⋅^n
where I is the current, A is the area of the loop, and ^n is the unit vector normal to the surface.
Face 1: BCFG
- The area A1 of face BCFG can be calculated as:
A1=l⋅l=l2
- The direction of the normal vector for this face is in the positive y-direction (J cap).
- Thus, the magnetic moment for face 1 is:
M1=I⋅A1⋅^n=I⋅l2⋅^J=Il2^J
Face 2: CFEG
- The area A2 of face CFEG is also:
A2=l⋅l=l2
- The direction of the normal vector for this face is in the positive x-direction (I cap).
- Thus, the magnetic moment for face 2 is:
M2=I⋅A2⋅^n=I⋅l2⋅^I=Il2^I
Face 3: BGHA
- The area A3 of face BGHA is:
A3=l⋅l=l2
- The direction of the normal vector for this face is in the negative x-direction (-I cap).
- Thus, the magnetic moment for face 3 is:
M3=I⋅A3⋅(−^I)=−I⋅l2⋅^I=−Il2^I
Step 3: Calculate the Total Magnetic Moment
Now, we can find the total magnetic moment M by summing the contributions from all three faces:
M=M1+M2+M3
Substituting the values we found:
M=(Il2^J)+(Il2^I)+(−Il2^I)
Step 4: Simplify the Expression
The contributions from M2 and M3 cancel each other out:
M=Il2^J+(Il2−Il2)^I=Il2^J
Final Answer
Thus, the total magnetic dipole moment of the closed path is:
M=Il2^J
---
The closed path abcdefgha consists of 8 edges of length l. We can divide this path into three distinct faces:
1. Face 1: BCFG
2. Face 2: CFEG
3. Face 3: BGHA
The magnetic dipole moment M for a current-carrying loop is given by the formula:
M=I⋅A⋅^n
where I is the current, A is the area of the loop, and ^n is the unit vector normal to the surface.
- The area A1 of face BCFG can be calculated as:
A1=l⋅l=l2
- The direction of the normal vector for this face is in the positive y-direction (J cap).
- Thus, the magnetic moment for face 1 is:
M1=I⋅A1⋅^n=I⋅l2⋅^J=Il2^J
- The area A2 of face CFEG is also:
A2=l⋅l=l2
- The direction of the normal vector for this face is in the positive x-direction (I cap).
- Thus, the magnetic moment for face 2 is:
M2=I⋅A2⋅^n=I⋅l2⋅^I=Il2^I
- The area A3 of face BGHA is:
A3=l⋅l=l2
- The direction of the normal vector for this face is in the negative x-direction (-I cap).
- Thus, the magnetic moment for face 3 is:
M3=I⋅A3⋅(−^I)=−I⋅l2⋅^I=−Il2^I
Now, we can find the total magnetic moment M by summing the contributions from all three faces:
M=M1+M2+M3
Substituting the values we found:
M=(Il2^J)+(Il2^I)+(−Il2^I)
The contributions from M2 and M3 cancel each other out:
M=Il2^J+(Il2−Il2)^I=Il2^J
Thus, the total magnetic dipole moment of the closed path is:
M=Il2^J
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example25videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.122videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
Similar Questions
A conductor carries a constant current I along the closed path abcdefgha involving S of the 12 edges each of length 1. Find the magnetic dipole moment of the closed path.
 View Solution
View SolutionAn electron moves with a constant speed v along a circle of radius r.(a) find the equivalent current through a point on its path.(b) Find the magnetic moment of the circulating electron.(c ) Find the ratio of the magnetic moment to the angular momentum of the electron.
View SolutionA circular coil of closely wound N terns and radius r carriers a current I.
Write the expressions for the following :
(i) the magnetic field at its centre
(ii) the magnetic moment of this coilView SolutionA current I flows in a conducting wire of lenth L. If we bent it in a circular form, then calculate its magnetic dipole moment.
View SolutionAnswer the following:
(a)Define SI unit of current in terms of the force between two parallel current carrying conductors.
(b) Two long straight parallel conductors carrying steady currents IaandIb along the same direction are separated by a distance d. How does one explain the force of attraction between them? If a third conductor carrying a current Ic in the opposite direction is placed just in the middle of these conductors , find the resultant force acting on the third conductor.View SolutionA wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View Solution
A conductor (shown in the figure) carrying constant current I is kept in the x-y plane in a uniform magnetic field B. If F is the magnitude of the total magnetic force acting on the conductor, then the correct statement is/are
View SolutionA conductor (shown in the figure) carrying constant current I is kept in the x−y plane in a uniform magnetic field →B. If →F is the magnitude of the total magnetic force acting on the conductor, then the correct statement(s) is (are)
 View Solution
View SolutionA conductor carrying current I is of the type as shown in figure. Find the magnetic field induction at the common centre O of all the three arcs.
 View Solution
View Solution

