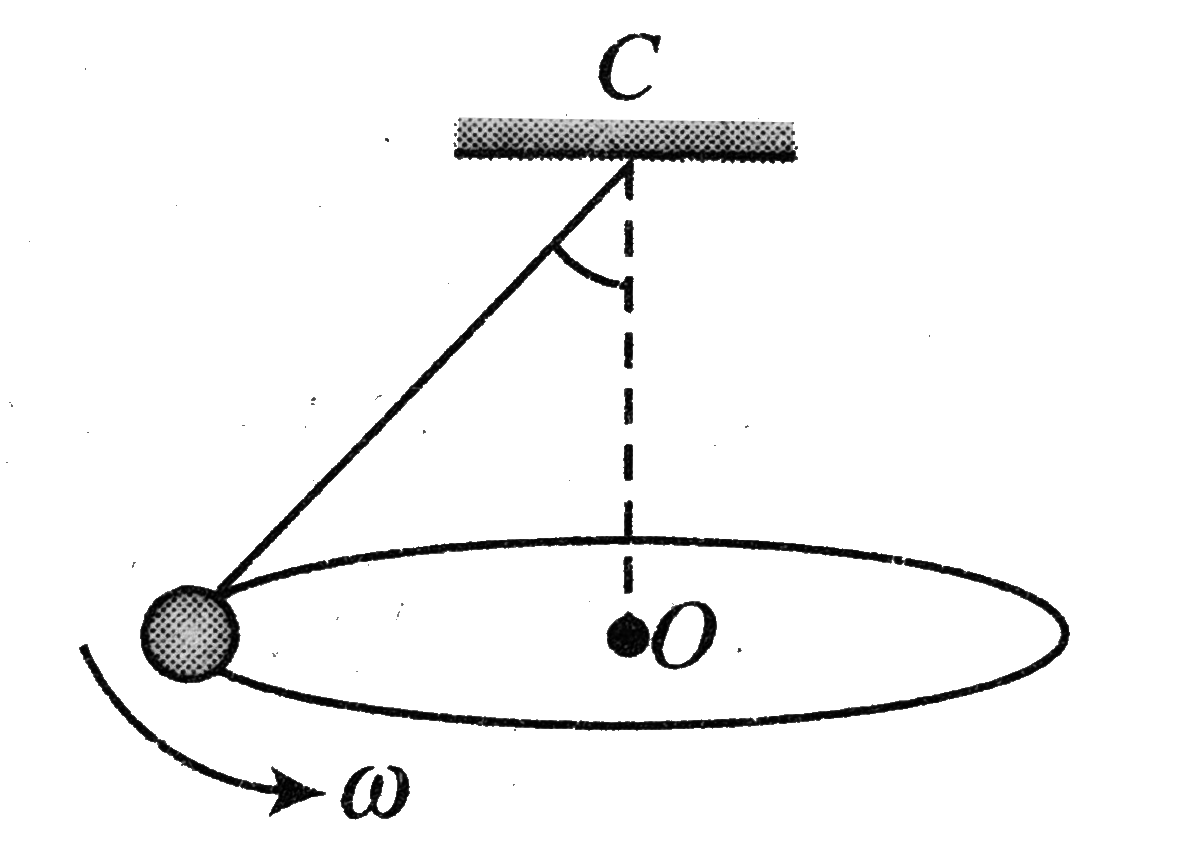
A conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω the constant angular velocity of the bob. If →L is the angular momentum about point C, then
→L is constant
only direction of →L is constant
only magnitude of →L is constant
none of the above
The correct Answer is:C
The distance of →L is perpendicular to the line joining the bob at point C. Since this line keeps changing its orientation is space, direction of →L keeps changing, however, as ω is constant, magnitude of →L remains constant.
Method 2 The torque about point is perpendicular to te angular momentum vector about point C. hence it can only change the directon of L and not its magnitude.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
Knowledge Check
- Question 1 - Select One
A conical pendulum consists of a bob of mass m in motion in a circular path in a horizontal plane as shown in figure. During the motion, the supporting wire of length l. Maintains a constant angle θ with the vertical. The magnitude of the angular momentum of the bob about the vertical dashed line is.
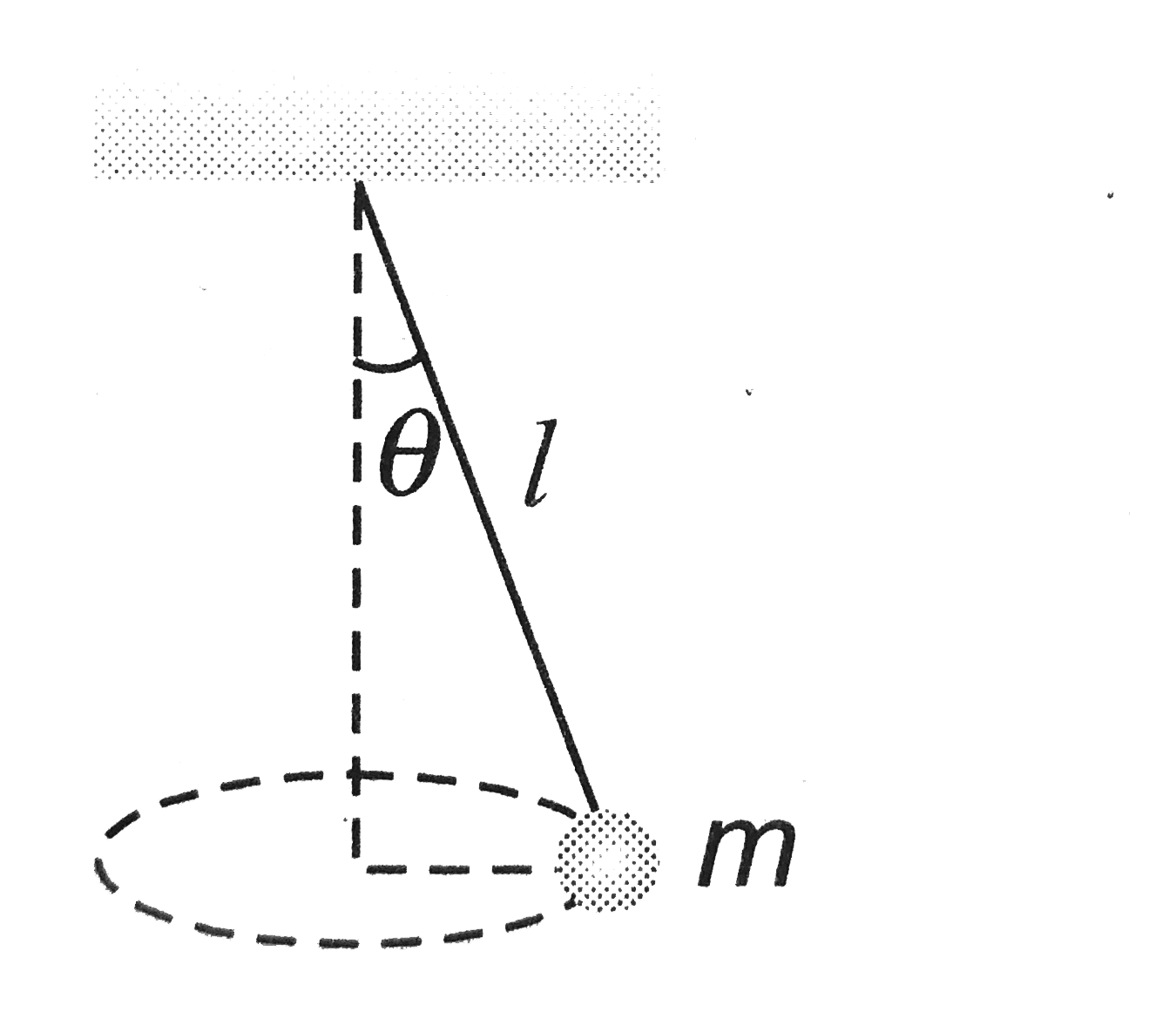 .A(m2gl3cos4θsinθ)1/2B(m2gl3cos4θcosθ)1/2C(m2gl3sin3θcosθ)1/2D(m2gl3cos3θcosθ)1/2.
.A(m2gl3cos4θsinθ)1/2B(m2gl3cos4θcosθ)1/2C(m2gl3sin3θcosθ)1/2D(m2gl3cos3θcosθ)1/2. - Question 2 - Select One
When the bob of a conical pendulam is moving in a horizontal circle at constant speed, which quantity is fixed?
AvelocityBAccelerationCCentripetal forceDKinetic energy - Question 3 - Select One
A particle P is moving in a circle of radius a with a uniform speed u, C is the centre of the circle and AB is a diameter. The angular velocities of P about A and C are in the ratio
A1:1B1:2C2:1D4:1
The angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
View SolutionA particle is moving with constant speed in a circle as shown in (Fig. 5.163). Find the angular velocity of the particle A with respect to fixed point BandC if angular velocity with respect to Oisω.
 .View Solution
.View SolutionA particle P is moving in a circle of radius r with a uniform speed u. C is the centre of the circle and AB is diameter. The angular velocity of P about A and V are in the ratio :
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
 View Solution
View SolutionTwo particle A and B are moving as shown in the figure
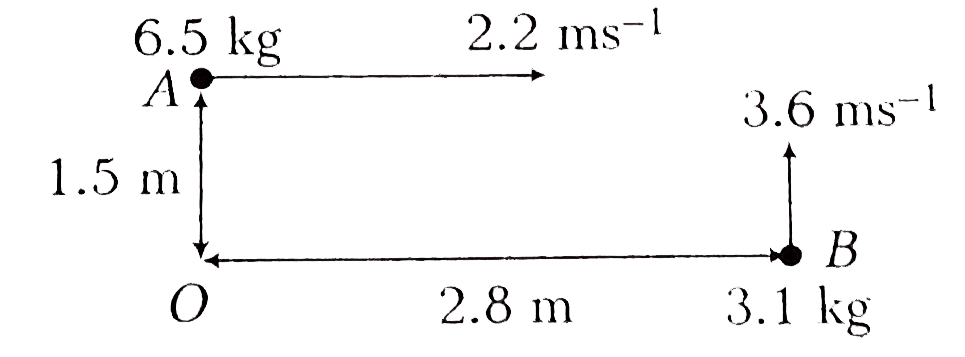
Their total angular momentum about the point O isView Solution