A constant force of 2.50 N accelerates a stationary particle of mass 15 g through a displacement of 2.50 m. Find the work done and the average power delivered.
The correct Answer is:A, B, C
To solve the problem, we will follow these steps:
Step 1: Convert the mass from grams to kilograms
The mass of the particle is given as 15 g. Since the SI unit of mass is kilograms, we need to convert grams to kilograms.
Mass=15g=151000kg=0.015kg
Step 2: Calculate the work done by the force
The work done (W) by a constant force can be calculated using the formula:
W=F⋅d
where:
- W is the work done,
- F is the force applied (2.50 N),
- d is the displacement (2.50 m).
Substituting the values into the formula:
W=2.50N⋅2.50m=6.25J
Step 3: Calculate the average power delivered
Average power (P) can be calculated using the formula:
P=Wt
where:
- P is the average power,
- W is the work done (6.25 J),
- t is the time taken to do the work.
To find the time taken, we first need to find the acceleration (a) using Newton's second law:
F=m⋅a⟹a=Fm
Substituting the values:
a=2.50N0.015kg=166.67m/s2
Now, we can use the kinematic equation to find the time taken (t) for the displacement (d):
d=12at2
Rearranging to find t:
t2=2da⟹t=√2da
Substituting the values:
t=√2⋅2.50m166.67m/s2=√5.00166.67≈√0.030≈0.173s
Now we can calculate the average power:
P=6.25J0.173s≈36.1W
Final Answers:
- Work done: 6.25J
- Average power delivered: 36.1W
---
The mass of the particle is given as 15 g. Since the SI unit of mass is kilograms, we need to convert grams to kilograms.
The work done (W) by a constant force can be calculated using the formula:
- W is the work done,
- F is the force applied (2.50 N),
- d is the displacement (2.50 m).
Average power (P) can be calculated using the formula:
- P is the average power,
- W is the work done (6.25 J),
- t is the time taken to do the work.
- Work done: 6.25J
- Average power delivered: 36.1W
Topper's Solved these Questions
Similar Questions
A tangential force of F = 1.5 N acts on a particle of mass m = 2 kg revolving in a circular path of radius r = 3 m. What is the work done by the torque for a complete revolution of the particle ?
View SolutionA cord is used to lower vertically a block of mass M through a distance d at a constant acceleration g/4. Find the work done by the cord on the block.
View Solution
Knowledge Check
A constant force (F) is applied on a stationary particle of mass 'm' The velocity attained by the particle in a certain displacement will be proportional to .
AmB1/mC√mD1√mA constant force (F) is applied on a stationary particle of mass 'm'. The velocity attained by the particle in a certain displacement will be proportional to
AmB1/mC√mD1√mA horizontal force of 10 N displaces a 5kg object through a distance of 2m in the direction of force. The work done by the force will be ________.
A20 JB10 JC5 JD50 J
Force acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
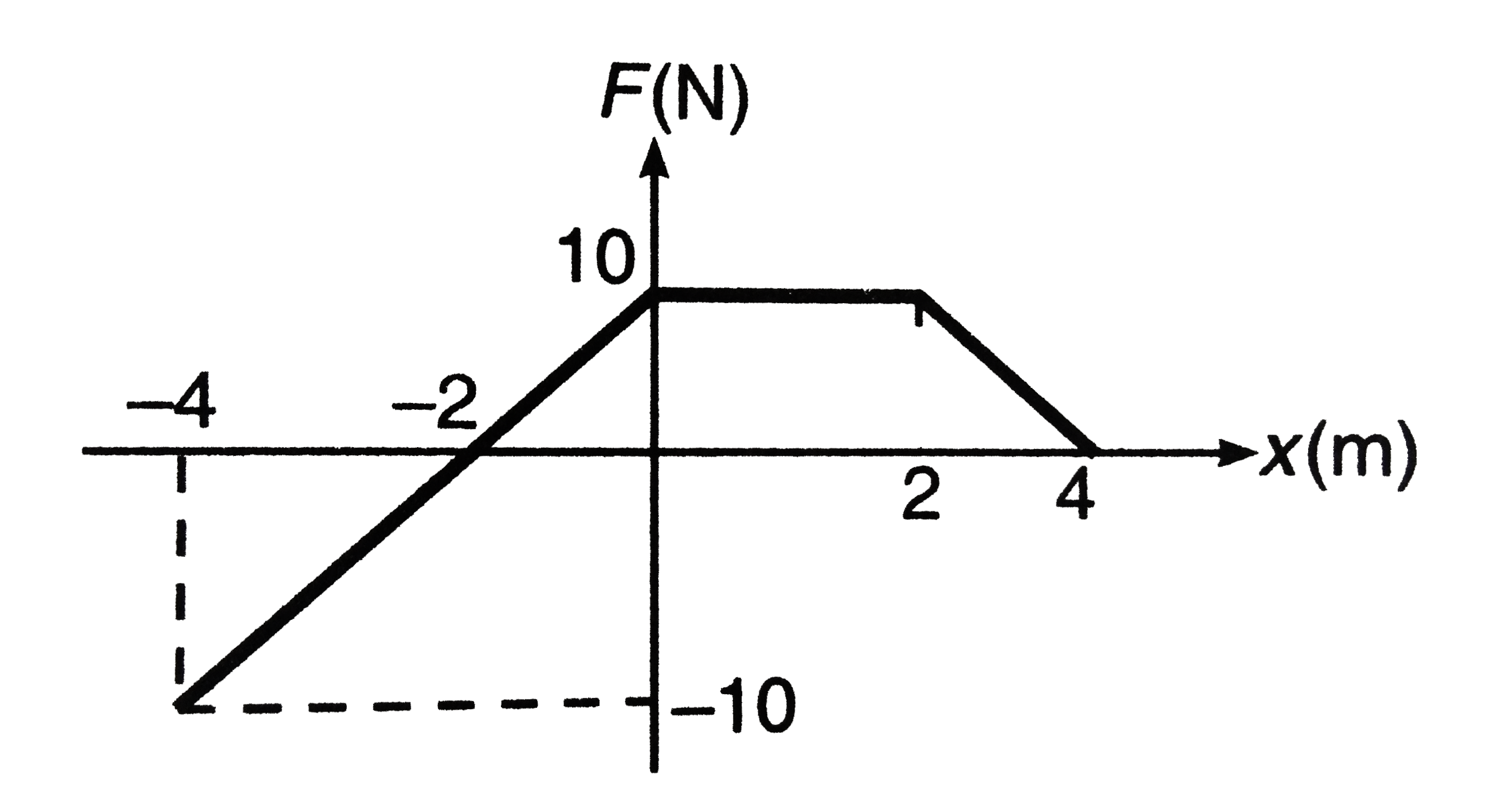 .
.
View SolutionA constant power P is applied on a particle of mass m. find kinetic energy, velocity and displacement of particle as function of time t.
View SolutionA force of 5 N is acting on an object. The object is displaced through 2 m in the direction of the force (Fig. 11.2). If the force acts on the object all through the displacement, then work done is 5N×2m=10N m or 10J.
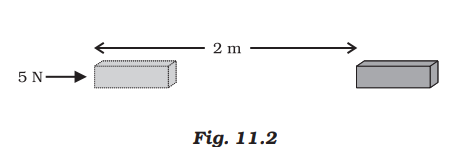
View SolutionA body, acted upon by a force of 50N, is displaced through a distance 10m in direction making an angle of 60∘ with the force. Find the work done by the force.
View SolutionIf a person moves a trolley for a distance of 10 m with a force of 50 , then the work done is:
View Solution
