A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
v=√g3[3H+4h]
v=√g3[4H−3h]
v=√g3[3H−4h]
None of these
The correct Answer is:C
Applying Bernoulli's equation just inside and just outside the hole.
p0+(H2)(d)g+(H2−h)(2d)(g)=12(2d)v2+p0
∴v=√g2(3H−4h).
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Subjective
Explore 24 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Example 13.1
Explore 1 Video
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Level 2 More Than One Correct
Explore 10 Videos
- EXPERIMENTSBook:DC PANDEYChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
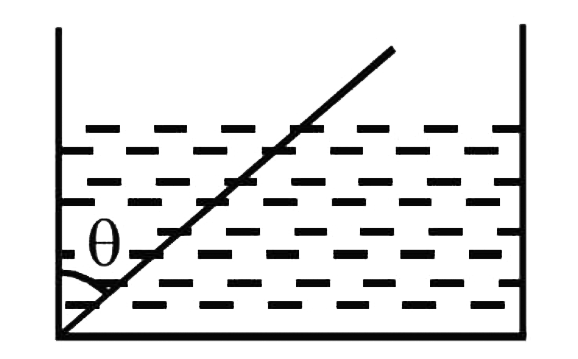
A wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
View SolutionAn open container has dimensions of 4.0m×5.0m and height of 3.0 m.
(i) Find the weight of the air in the container at 20∘C.
(ii) What is the weight of an equal volume of water ? Also find pressure at the base of container due to this weight pof water.
(iii) What is the total downward force on the base of the container due to air pressure of 1.0 atm ?
Take the denities of air and water as 1.2kg/m3 and 103kg/m3 respectively.
View SolutionA large wooden plate of area 10m2 floating on the surface of river is made to move horizontally wilth a speed of 2ms−1 by applying a tangential force. If the river is 1m deep and the water contact with the bed is stationary, find the tangential force needed to keep the plate moving. Coefficient of viscosity of water at the temperature of the river =10−2poise.
View SolutionIn a meter bridge set up, which of the following should be the properties of the one meter long wire?
View SolutionIf the dimensions of B2l2C are [MaLbTc], then the value of a+b+c is
[Here B,l and C represent the magnitude of magnetic field, length and capacitance respectively]
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P_0 . Then density D of solid is given by
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The density D of the material of the floation cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial value of x is
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d , each of height H//2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L lt (H)/(2)) , cross-sectional area A//5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L//4 denser liquid. Determine (a) density D of the solid and (b) the total pressure at the bottom of the container. (Atmospheric pressure = P_0 ). .
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two-immiscible, non-viscous & incompressible liquids of densities d & 2d, each of height H/2. The lower density liquid is open to the atmoshpere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) corss-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid interface with the length L/4 in the denser liquid. Determine : (i) The density D of the solid & (ii) The total pressure at the bottom of the container.
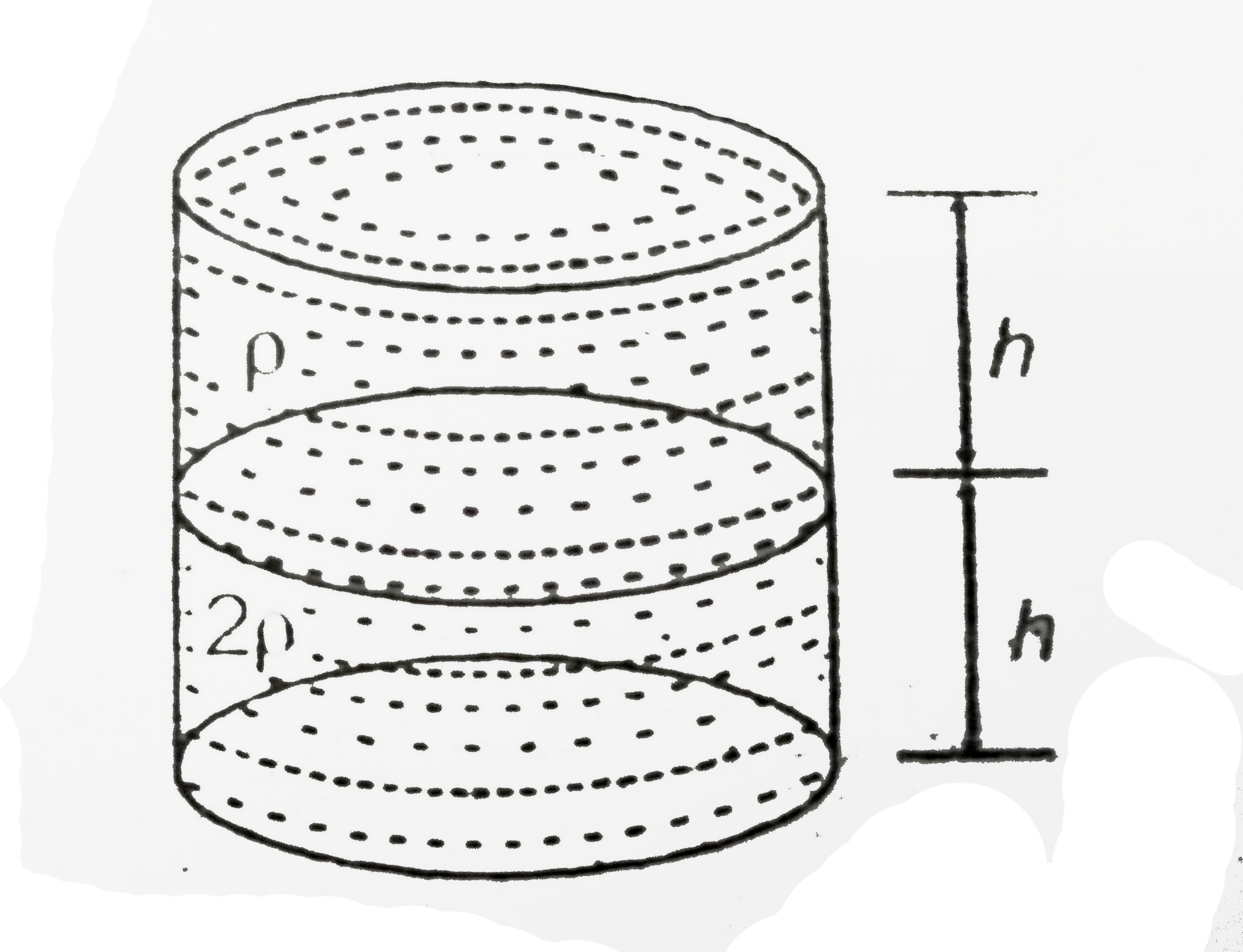
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View SolutionA vessel of large uniform cross-sectional area resting on a horizontal surface holds two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2. If a small hole is punched on the vertical side of the container at a heighth h(h<H2) the efflux speed of the liquid al the hole is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The density D of the material of the floating cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial speed of efflux without cylinder is
View Solution