A container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
P2,T
P2,T2
P, T
P,T2
The correct Answer is:A
To solve the problem of what happens when the valve is suddenly opened in a container divided into two equal parts, we can follow these steps:
1. Understanding the System:
- We have a container divided into two equal parts by a partition.
- One part contains an ideal gas at pressure P and temperature T.
- The other part is a vacuum (completely evacuated).
2. Opening the Valve:
- When the valve is opened, the gas will expand into the vacuum. This is known as free expansion.
3. Characteristics of Free Expansion:
- In free expansion, the gas does not perform work on the surroundings, and since the walls are insulating, there is no heat exchange with the environment.
- Therefore, the process is adiabatic, and the internal energy of the gas remains constant.
4. Temperature Change:
- For an ideal gas undergoing free expansion, the temperature remains constant. Hence, the final temperature T′ of the gas after expansion will still be T.
5. Pressure Change:
- Initially, the volume of the gas is V/2 (where V is the total volume of the container).
- After the gas expands to fill the entire volume V, we can use the ideal gas law, which states that PV=nRT.
- Initially, we have:
P⋅V2=nRT
- After expansion, the new pressure P′ can be calculated as:
P′⋅V=nRT
- By equating the two expressions for nRT:
P⋅V2=P′⋅V
- Simplifying this gives:
P′=P2
6. Final Results:
- After the valve is opened, the pressure of the gas will be P2 and the temperature will remain T.
Conclusion:
- The final pressure of the gas is P2 and the final temperature is T.
- We have a container divided into two equal parts by a partition.
- One part contains an ideal gas at pressure P and temperature T.
- The other part is a vacuum (completely evacuated).
- When the valve is opened, the gas will expand into the vacuum. This is known as free expansion.
- In free expansion, the gas does not perform work on the surroundings, and since the walls are insulating, there is no heat exchange with the environment.
- Therefore, the process is adiabatic, and the internal energy of the gas remains constant.
- For an ideal gas undergoing free expansion, the temperature remains constant. Hence, the final temperature T′ of the gas after expansion will still be T.
- Initially, the volume of the gas is V/2 (where V is the total volume of the container).
- After the gas expands to fill the entire volume V, we can use the ideal gas law, which states that PV=nRT.
- Initially, we have:
P⋅V2=nRT
- After expansion, the new pressure P′ can be calculated as:
P′⋅V=nRT
- By equating the two expressions for nRT:
P⋅V2=P′⋅V
- Simplifying this gives:
P′=P2
- After the valve is opened, the pressure of the gas will be P2 and the temperature will remain T.
- The final pressure of the gas is P2 and the final temperature is T.
Topper's Solved these Questions
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Multiple choice questions-II
8 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Multiple choice questions-III
12 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Problems for practice
47 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
Similar Questions
A nonconducting cylinder having volume 2V0 is partitioned by a fixed non conducting wall in two equal part. Partition is attached with a valve. Right side of the partition is a vacuum and left part is filled with a gas having pressure and temperature P0 and T0 respectively. If valve is opened find the final pressure and temperature of the two parts.
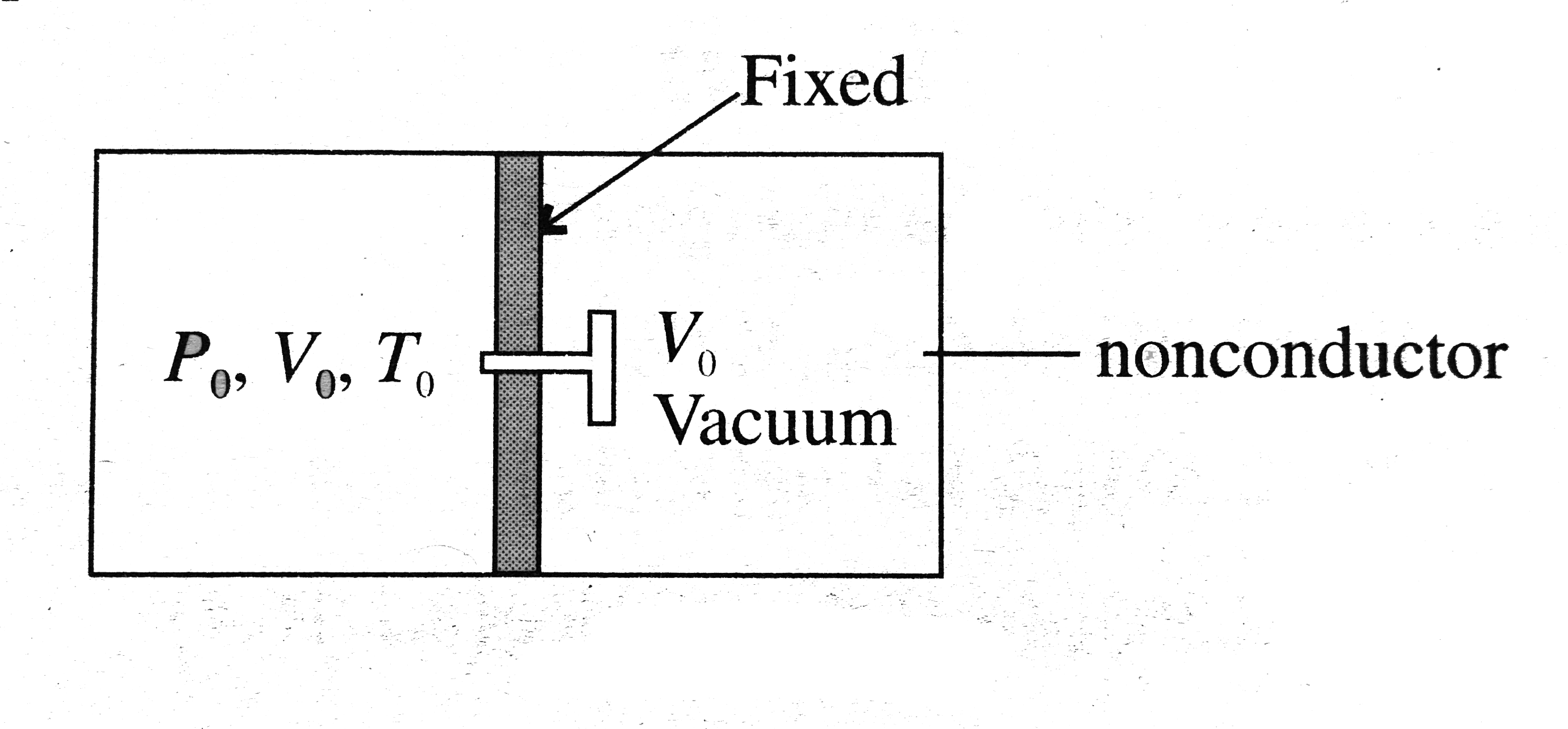
View SolutionAn insulated container is divided into two equal portions. One portion contains as ideal gas at pressure P and tenperature T. The other portion is a perfect vaccum. If a hole is opened between the two portions, claculate
a. the change in internal energy.
b. the change in temperature.
View Solution
Knowledge Check
An insulated container is divided into two equal portions.One portion contains an ideal monoatomic gasat pressue P and temperature. T while the other protion is a perfect vacuum. If a hole is opened between the two portion, the change in internal energy of the gas is
AzeroBequal to work done by the gasCequal to work done on the gasD3RT/2A given quantity of a ideal gas is at pressure P and absolute temperature T. The isothermal bulk modulus of the gas is
A23PBPC32PD2PAn insulated container of gas has two chambers separated by an insulating partition. One of the chmabers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
A(T1T2P1V1+P2V2P1V1T2+P2V2T1BP1V1T1+P2V2T2P1V1+P2V2CP1V1T2+P2V2T1P1V1+P2V2DT1T2(P1V1+P2V2)P1V1T1+P2V2T2
Two cylinders A and B of equal capacity are connected to each other vis a stop cock. A contains an ideal gas at standard temperature and pressure. B is completely evacuated. The sto cock is suddenly opened. The process is:
View SolutionAn insulated container is divided into two equal portions. One portion contains as ideal gas at pressure P and tenperature T. The othe portion is a perfect vaccume. If a hole is opened between the two portions, claculate
a. the change in internal energy.
b. the change in temperature.
View SolutionA container of volume 1m3 is divided into two equal parts by a partition. One part has an ideal gas at 300K and the other part is vacuum. The whole system is thermally isolated from the surroundings. When the partition is removed, the gas expands to occupy the whole volume. Its temperature will now be .......
View SolutionA container of volume 1m3 is divided into two equal parts by a partition. One part has an ideal gas at 300K and the other part is vacuum. The whole system is thermally isolated from the surroundings. When the partition is removed, the gas expands to occupy the whole volume. Its temperature will now be .......
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chambers has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partion is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View Solution
