A convex lens is placed over a plane mirror. A pin is now positioned so that there is no parallax between the pin and its image formed by this lens-mirror combination. How can this observation be used to find the focal length of the convex lens? Give appropriate reasons in support of your answer.
To find the focal length of a convex lens placed over a plane mirror using the observation of a pin and its image, we can follow these steps:
1. Setup the Experiment: Place a convex lens on top of a plane mirror. Position a pin (object) in front of the lens at a certain distance.
2. Adjust the Position of the Pin: Move the pin until there is no parallax between the pin and its image formed by the lens-mirror combination. This means that the pin and its image coincide tip-to-tip.
3. Understanding the Image Formation: When the pin and its image coincide, it indicates that the rays of light coming from the pin are being refracted by the lens and then reflected by the mirror in such a way that they retrace their path back through the lens.
4. Analyzing Ray Paths: Draw a ray diagram to visualize the situation. Consider two rays emanating from the pin:
- One ray goes through the optical center of the lens and continues straight to the mirror.
- The second ray is refracted by the lens and converges to a point on the opposite side of the lens.
5. Condition for No Parallax: For there to be no parallax, the rays must be parallel after reflection from the mirror. This occurs when the angle of incidence on the mirror is zero, meaning the rays must hit the mirror normally.
6. Identifying the Focal Point: Since the rays are parallel after reflection, they must converge at the focal point of the lens. The distance from the optical center of the lens to the focal point is the focal length (f) of the lens.
7. Measuring the Distance: Measure the distance from the pin (object) to the mirror (let's call this distance OT). Since the rays retrace their path and the object and image coincide, this distance OT is approximately equal to the focal length of the lens.
8. Conclusion: Therefore, by measuring the distance OT (from the pin to the mirror), we can determine the focal length of the convex lens.
Final Result:
The focal length (f) of the convex lens can be found using the relationship:
f≈OT
where OT is the distance from the pin to the mirror when there is no parallax.
- One ray goes through the optical center of the lens and continues straight to the mirror.
- The second ray is refracted by the lens and converges to a point on the opposite side of the lens.
The focal length (f) of the convex lens can be found using the relationship:
f≈OT
where OT is the distance from the pin to the mirror when there is no parallax.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (1)
13 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (2)
9 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A convex lens is placed in contact with a plane mirror. An axial point object at a distance of 20cm from this combination, has its image coinciding with itself. What is the focal length of the convex lens ?
View SolutionDraw ray diagrams showing the image formation by a concave lens when an object is placed
(a) between focus and twice the focal length of the lens
(b) beyond twice the focal length of the lens
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirrorA convex lens of focal length 15 cm is placed on a plane mirror. An object is placed 20 cm from the lens. The image is formed
A12 cm in front of the mirrorB60 cm behind the mirrorC60 cm in front of the mirrorD30 cm in front of the mirror
A convex lens is placed in contact with a plane mirror. An axial point object at a distance of 20cm from this combination, has its image coinciding with itself. What is the focal length of the convex lens ?
View SolutionA convex lens is placed in contact with a plane mirror. A point object at a distance of 20 cm on the axis of this combination has its image coinciding with itself. What is the focal length of the lens ?
View SolutionThe same size images are formed by a convex lens when the object is placed at 20cm or at 10cm from the lens. The focal length of convex lens is ____ cm
View SolutionAnalyse the following observation table showing variation of image distance (v) with object distance (u) in case of a convex lens and answer the questions that follow, without doing any calculation :
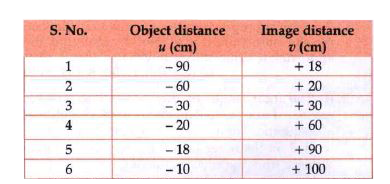
What is the focal length of the convex lens? Give reason in support of your answer.
View SolutionA convex lens of focal length 15cm, and a concave mirror of radius of curvature 20cm are placed co-axially 10cm apart. An object is placed in front of convex lens so that there is no parallax between the object and its image formed by the combination. Find the position of the object.
View SolutionA thin convex lens of focal length 'f' is put on a plane mirror as shown in the figure . When an object is kept at a distance 'a' from the lens - mirror combination , its image is formed at a distance a3 in front of the combination . The value of 'a' is :-
_E01_189_Q01.png)
View Solution
