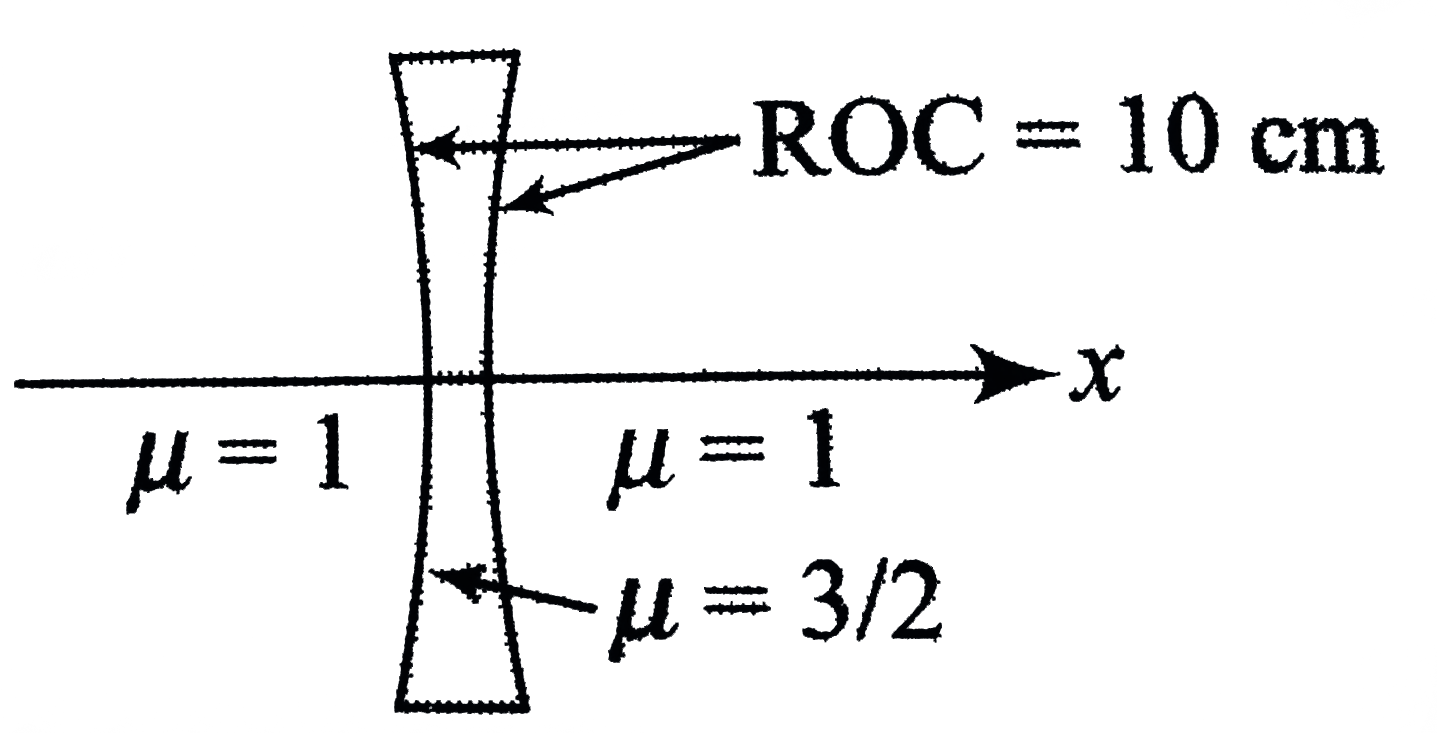A convex lens of focal length f cut into parts first horizontally and then vertically. Find the focal length of part A of the lens, as shown:
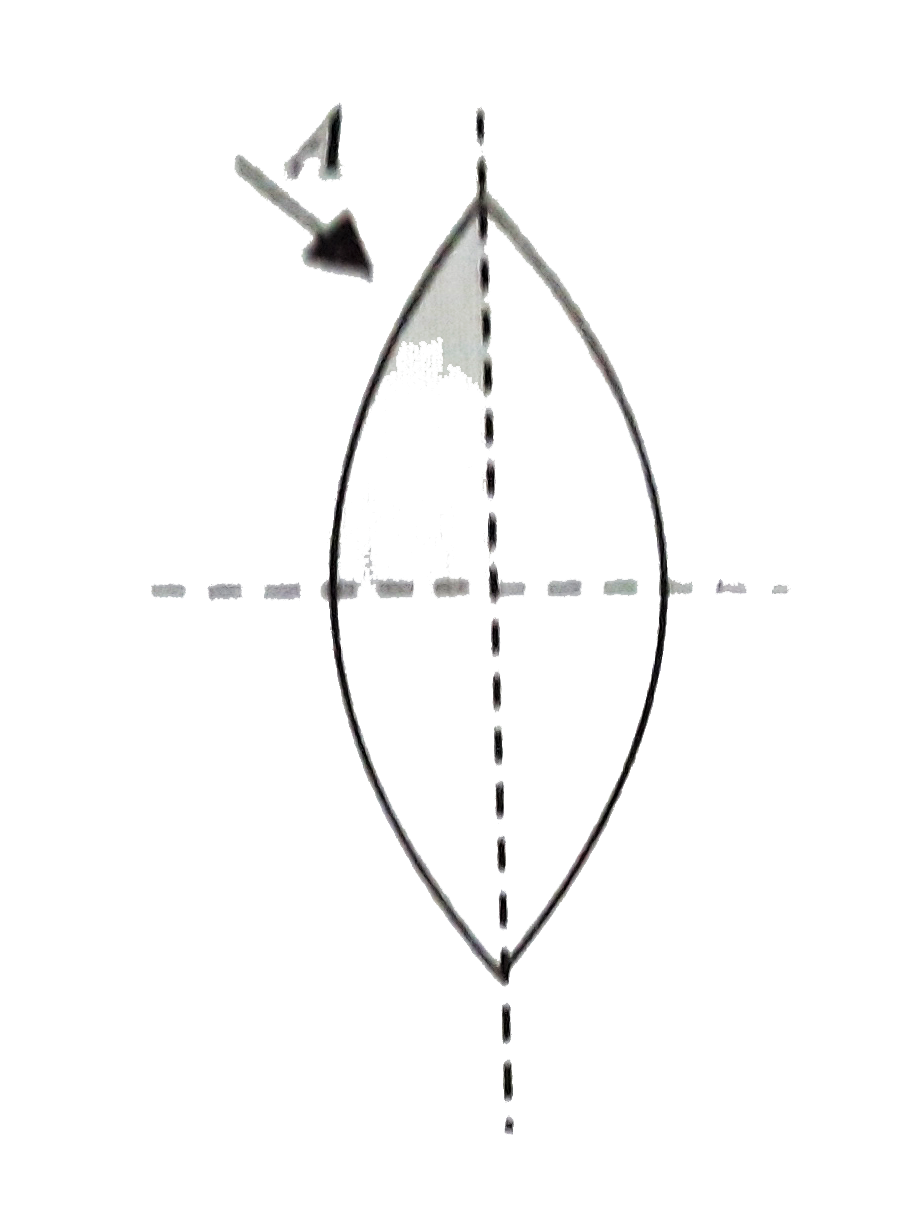
f/2
f
4f
2f
The correct Answer is:d.
When cut horizontally, focal length remains same as is clear from the following formula:
1f=(μ−1)[1R−1(−R)]=2(μ−1)R (i)
When cut vertically, focal length is doubled.
1f′=(μ−1)[1R−1∞]=(μ−1)R=12f
Combining these factors,
f′=2f
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Knowledge Check
A plano convex lens has focal length f=20cm. If its plane surface is silvered, then new focal length will be
A20cmB40 cmC30 cmD10 cm
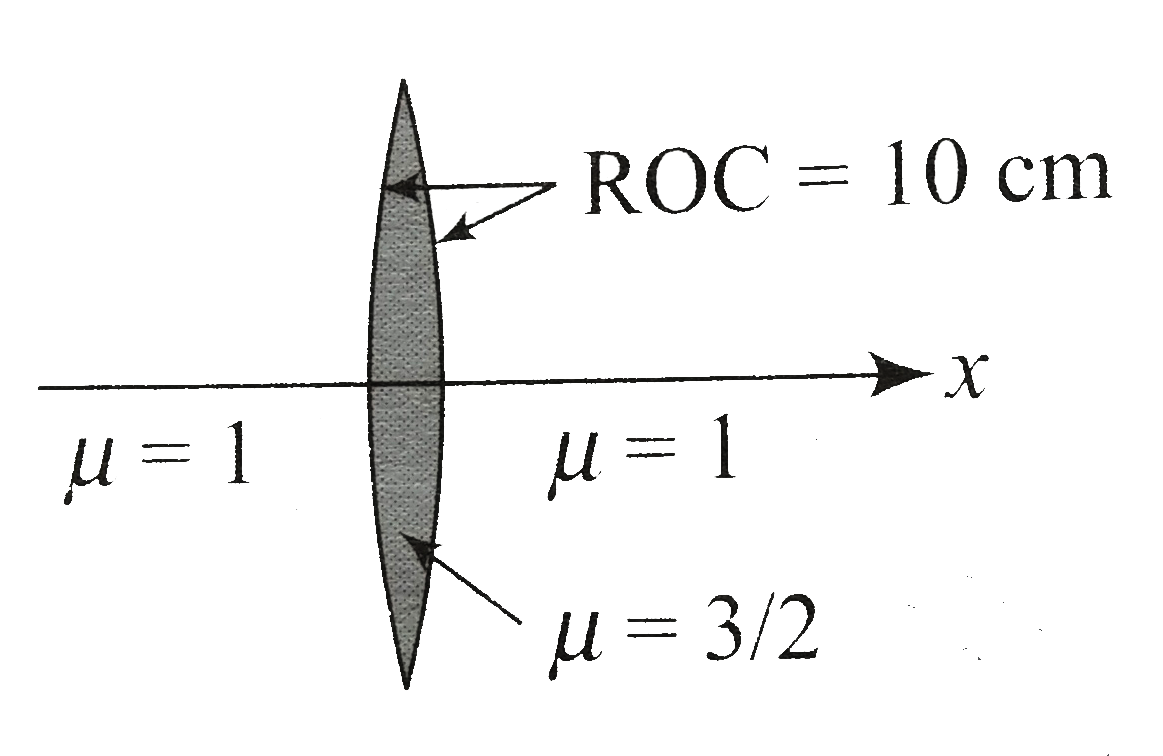
Find the focal length of the lens shown in the Fig..
View SolutionAn equiconvex lens of focal length 15cm is cut into two equal halves in thickness. What is the focal length of each half ?
View SolutionA convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
View SolutionA thin convex lens of focal length 20 cm is kept in contact with a thin concave lens of focal length 15 cm. Find the focal length and the nature of the combination.
View SolutionA converging lens of focal length 40 cm is kept in contact with a diverging lens of focal length 30 cm. Find the focal length of the combination.
View SolutionA convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View Solution