A convex lens of focal length x and a concave lens of focal length y are placed in contact. The focal length of the combination is
(x + y)
(x - y)
xyx+y
xyy−x
The correct Answer is:D
To find the focal length of a combination of a convex lens and a concave lens placed in contact, we can follow these steps:
1. Identify the Focal Lengths:
- Let the focal length of the convex lens be f1=x (positive value).
- Let the focal length of the concave lens be f2=y (negative value).
2. Use the Lens Formula:
- The formula for the focal length f of two lenses in contact is given by:
1f=1f1+1f2
3. Substitute the Focal Lengths:
- Substitute f1 and f2 into the formula:
1f=1x+1y
4. Convert the Concave Lens Focal Length:
- Since the focal length of the concave lens is negative, we can write:
1f=1x−1y
5. Combine the Fractions:
- To combine the fractions, find a common denominator:
1f=y−xxy
6. Find the Focal Length of the Combination:
- Taking the reciprocal gives us the focal length of the combination:
f=xyy−x
Final Answer:
The focal length of the combination of the convex lens and concave lens placed in contact is:
f=xyy−x
- Let the focal length of the convex lens be f1=x (positive value).
- Let the focal length of the concave lens be f2=y (negative value).
- The formula for the focal length f of two lenses in contact is given by:
1f=1f1+1f2
- Substitute f1 and f2 into the formula:
1f=1x+1y
- Since the focal length of the concave lens is negative, we can write:
1f=1x−1y
- To combine the fractions, find a common denominator:
1f=y−xxy
- Taking the reciprocal gives us the focal length of the combination:
f=xyy−x
The focal length of the combination of the convex lens and concave lens placed in contact is:
f=xyy−x
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - MCGROW HILL PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING QUESTIONS
37 Videos
- REFLECTION OF LIGHT BOOK - MCGROW HILL PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - HIGHER ORDER THINKING QUESTIONS
10 Videos
- SOURCES OF ENERGY BOOK - MCGROW HILL PUBLICATIONCHAPTER - SOURCES OF ENERGY EXERCISE - ELEMENTARY QUESTIONS
82 Videos
Similar Questions
A convex lens of focal length 30 cm and a concave lens of focal length 0.6m are placed in contact. Find the power of the combination.
View SolutionA convex lens of focal length 18 cm and a concave lens of focal length 24 cm are placed in contact such that they have a common principal axis. Will the combination act as a convex lens or a concave lens ? Find the focal length and power of the combination .
View Solution
Knowledge Check
A convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
A(A+B)B(A-B)CAB(A+B)DAB(B−A)A convex lens of focal length 40 cm a concave lens of focal length 40 and a concave lens of focal length 15 cm are placed in contact. The power of this combination of are placed in contact. The power of this combination in diopters is
A+1.5B−1.5C+6.67D−6.67A convex lens of focal length 50 cm, a concave lens of focal length 50 cm and a concave lens focal lens 20 cm are placed in contact. The power of this combination in diopters will be
A−4.67DB−5DC−3.21DD−3D
A convex lens of focal length 25 cm and a concave lens of focal length 10 cm are placed in close contact with one another.
a) What is the power of this combination?
b) What is the focal length of this combination?
c) Is the combinatioin converging or diverging?
View Solution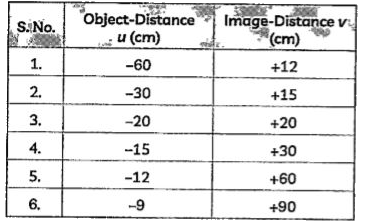
The focal length of the convex lens is
View SolutionA convex lens of focal length 25 cm and a concave lens of focal length 10 cm are joined together. The power of the combination will be
View SolutionA convex lens of focal length 10cm and concave lens of focal length 20cm are kept 5cm apart. The focal length of the equivalent lens is
View SolutionWe combined a convex lens of focal length f1 and concave lens of focal lengths f2 and their combined focal length was F . The combination of these lenses will behave like a concave lens, if
View Solution
