A cotton reel has a inner radius and outer radius . Mass of the reel is and moment of inertia about longitudinal rotational axis is . A force is applied at the free end of thread wraped of the reel as shown in fig. If the reel moves without sliding.

a. Determine the frictional force exerted by the table on the reel and the direction in which it acts.
b. In what direction does the reel begin to move?
Method 1: As the body rolls, point will be instantasneous centre of rotation (). There is clockwise torque about . Hecne centre of mass will have acceleratioin in eright direction. As there is net torque about in clockwise sense. Hence the reel will rotate in clockwise direction.

Hence the reel moves to the right. Force exerts anticlockwise torque, therefore friction force must exert a larger clockwise torque to produce clockwise rolling. The equations of the motion are
.....i
............ii
..............iii
As the reel rolls without slipping
From eqn i and iii we get
Force of friction comes out to be positive, therefore our assumption about the direction of friction force was correct. On substituting the expression for in Eqn i we obtain
As , a positive and towards right. Similarly, from eqn iii, we obtain
Which is positive i.e., net torque on the reel is clockwise.
Method 2: We can apply torque equation about.

ICR
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A cotton reel has a inner radius r and outer radius R. Mass of the reel is M and moment of inertia about longtudinal rotational axis is I. A force P is applied at the free end of thread wraped of the reel as shown in fig. If the reel moves without sliding.

a. Determine the frictioal force exerted by the table on the reel and the direction in which it acts.
b. I what direction does the reel begin to move?View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
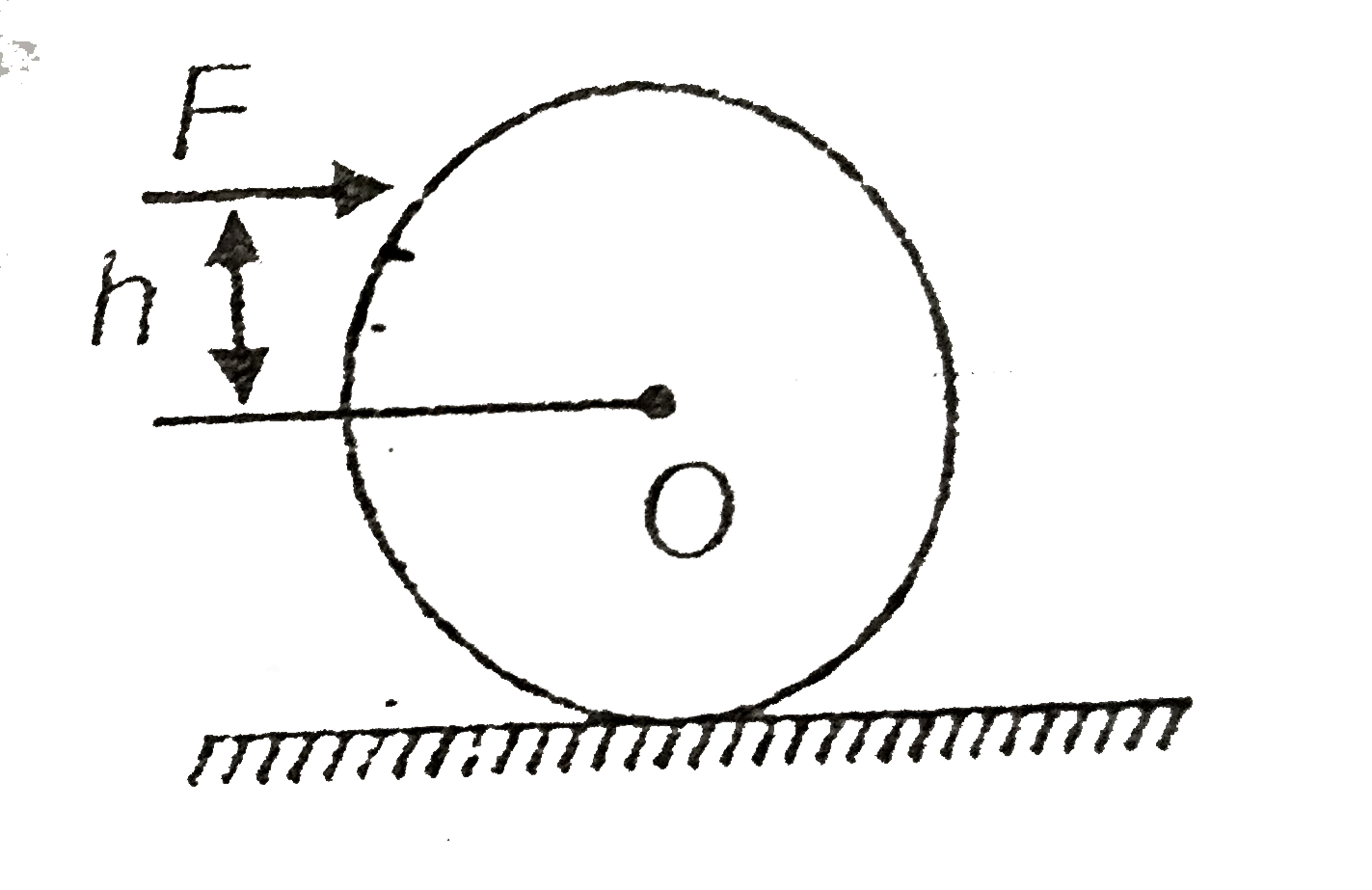 View Solution
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
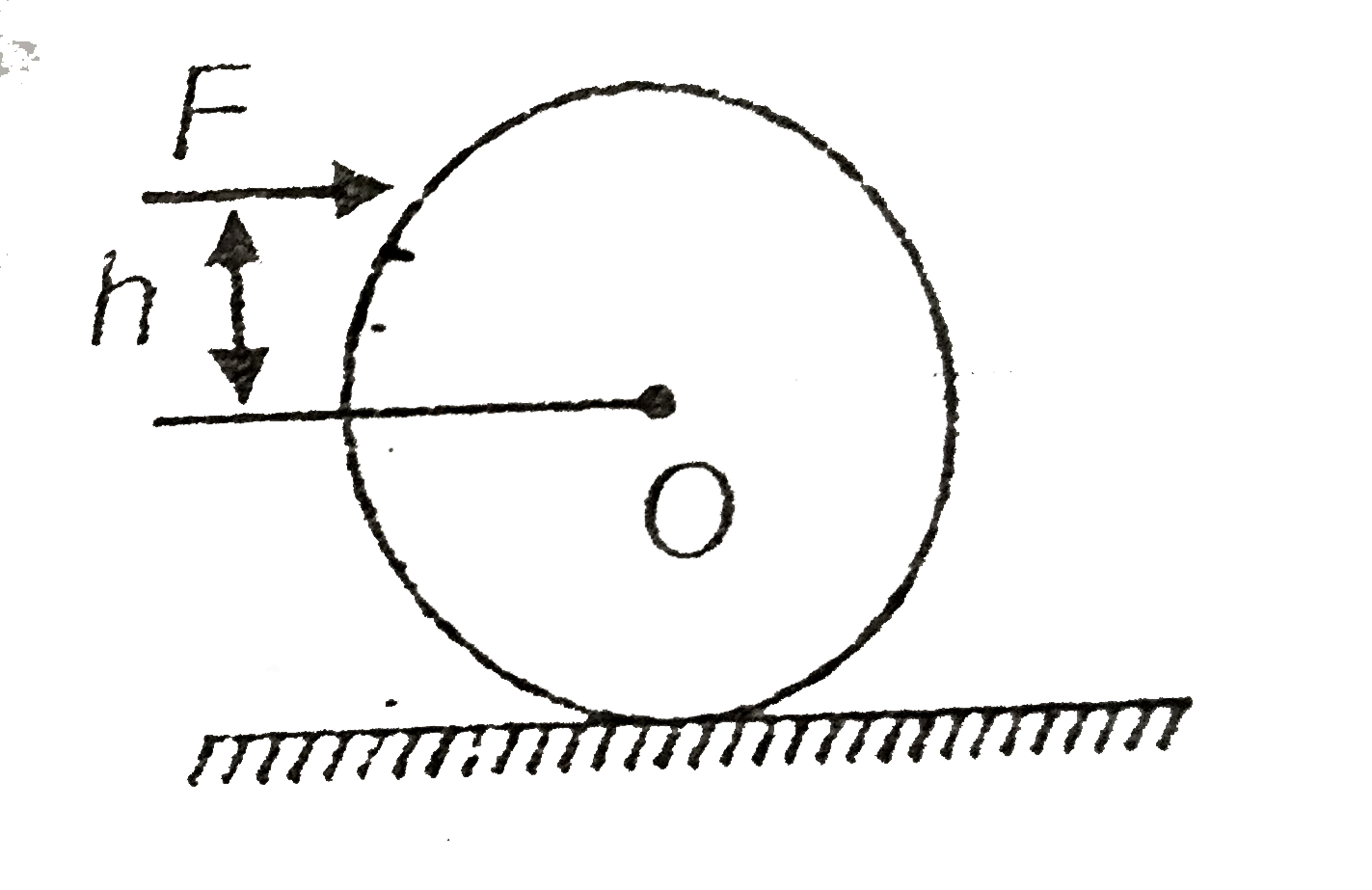 View Solution
View SolutionA spool has a mass of 2 kg,an inner radius R1 =3cm,and an outer radius R2=5cm, the radius of gyration about the axis of the spool is if=4cm.A constant horizontal force of 5N is applied to the free end of a massless thread that is wrapped around the inner cylinder of the spool as shownin figure-5.150. If the spool rolls without slipping, calculate the linear acceleration along the horizontal surface. What is the minimum coefficient of static friction required to prevent slipping ?
 View Solution
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View SolutionA wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
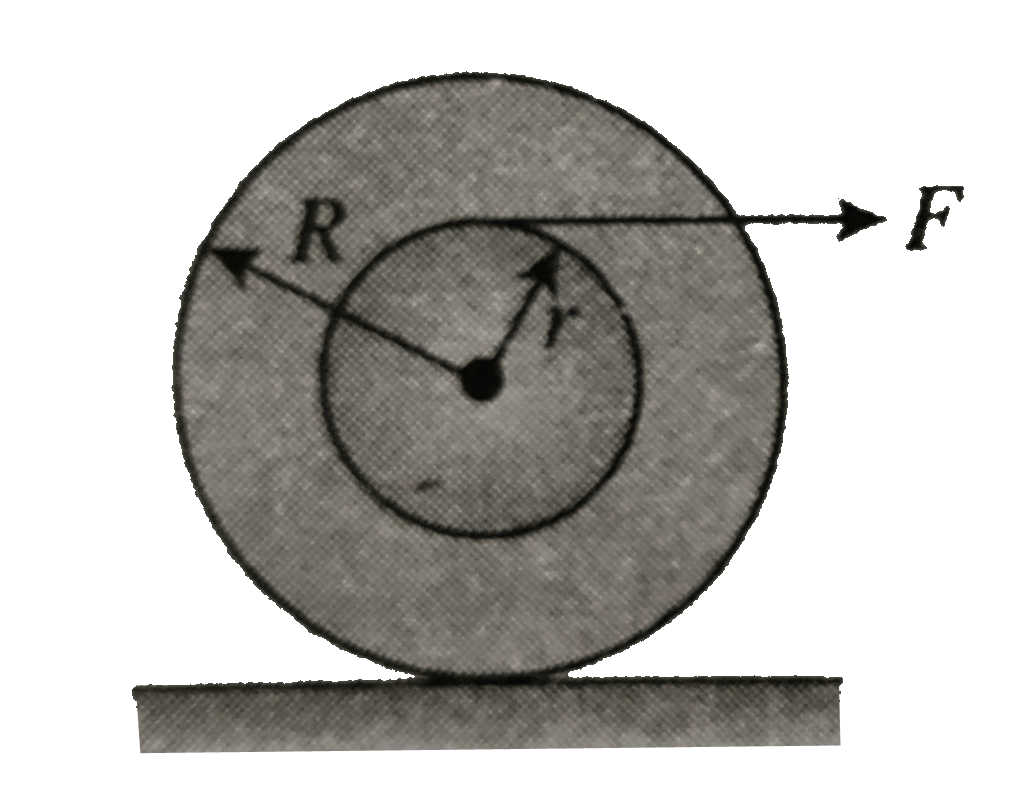
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.View SolutionA wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.

a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
 View Solution
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
 View Solution
View Solution

