A current carrying loop lies on a smooth horizontal plane. Then,
it is possible to establish a uniform magnetic field in the region so that the loop starts rotating about its own axis.
it is possible to establish a uniform magnetic field in the region so that the loop will tip over over about any of the point.
it is not possible that loop will tip over about any of the point whatever be the direction of established magnetic field (uniform).
both (a) and (b) are correct.
The correct Answer is:b
To solve the problem regarding the current-carrying loop on a smooth horizontal plane, we will analyze the effects of a magnetic field on the loop and determine the correct option based on the behavior of the loop under different magnetic field orientations.
1. Understanding the Setup:
- We have a current-carrying loop lying on a smooth horizontal plane. The loop can be represented in the XY-plane, with the Z-axis being vertical.
2. Magnetic Moment:
- The magnetic moment M of the loop is given by the formula:
M=n⋅I⋅A
where n is the number of turns (which is 1 for a single loop), I is the current, and A is the area vector of the loop, which is perpendicular to the plane of the loop.
3. Torque on the Loop:
- The torque τ acting on the loop due to an external magnetic field B is given by:
τ=M×B
- The torque will cause the loop to rotate if it is not aligned with the magnetic field.
4. Case 1: Magnetic Field in the X-direction:
- If the magnetic field B is in the X-direction, the angle between M (which is in the Z-direction) and B is 90 degrees. Thus, torque exists:
τ=M⋅B⋅sin(90∘)=M⋅B
- The torque will act in the plane of the loop, but it will not cause the loop to rotate about its own axis.
5. Case 2: Magnetic Field in the Y-direction:
- If B is in the Y-direction, M and B are parallel. Therefore, the torque is zero:
τ=M⋅B⋅sin(0∘)=0
- The loop will not rotate.
6. Case 3: Magnetic Field in the Z-direction:
- If B is in the Z-direction, M and B are perpendicular. Thus, torque exists:
τ=M⋅B⋅sin(90∘)=M⋅B
- The torque will act in the X-direction, which can cause the loop to tip over but not rotate about its own axis.
7. Conclusion:
- In all cases analyzed, the loop does not rotate about its own axis. However, it can tip over when the magnetic field is applied in the Z-direction. Therefore, the correct option is that it is possible to establish a uniform magnetic field in a region so that the loop will tip over about any point.
Final Answer:
The correct option is that it is possible to establish a uniform magnetic field in a region so that the loop will tip over about any point.
- We have a current-carrying loop lying on a smooth horizontal plane. The loop can be represented in the XY-plane, with the Z-axis being vertical.
- The magnetic moment M of the loop is given by the formula:
M=n⋅I⋅A
where n is the number of turns (which is 1 for a single loop), I is the current, and A is the area vector of the loop, which is perpendicular to the plane of the loop.
- The torque τ acting on the loop due to an external magnetic field B is given by:
τ=M×B
- The torque will cause the loop to rotate if it is not aligned with the magnetic field.
- If the magnetic field B is in the X-direction, the angle between M (which is in the Z-direction) and B is 90 degrees. Thus, torque exists:
τ=M⋅B⋅sin(90∘)=M⋅B
- The torque will act in the plane of the loop, but it will not cause the loop to rotate about its own axis.
- If B is in the Y-direction, M and B are parallel. Therefore, the torque is zero:
τ=M⋅B⋅sin(0∘)=0
- The loop will not rotate.
- If B is in the Z-direction, M and B are perpendicular. Thus, torque exists:
τ=M⋅B⋅sin(90∘)=M⋅B
- The torque will act in the X-direction, which can cause the loop to tip over but not rotate about its own axis.
- In all cases analyzed, the loop does not rotate about its own axis. However, it can tip over when the magnetic field is applied in the Z-direction. Therefore, the correct option is that it is possible to establish a uniform magnetic field in a region so that the loop will tip over about any point.
The correct option is that it is possible to establish a uniform magnetic field in a region so that the loop will tip over about any point.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View SolutionAn infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its centre from the wire is d (d>>a). If the loop applies a force F on the wire then :
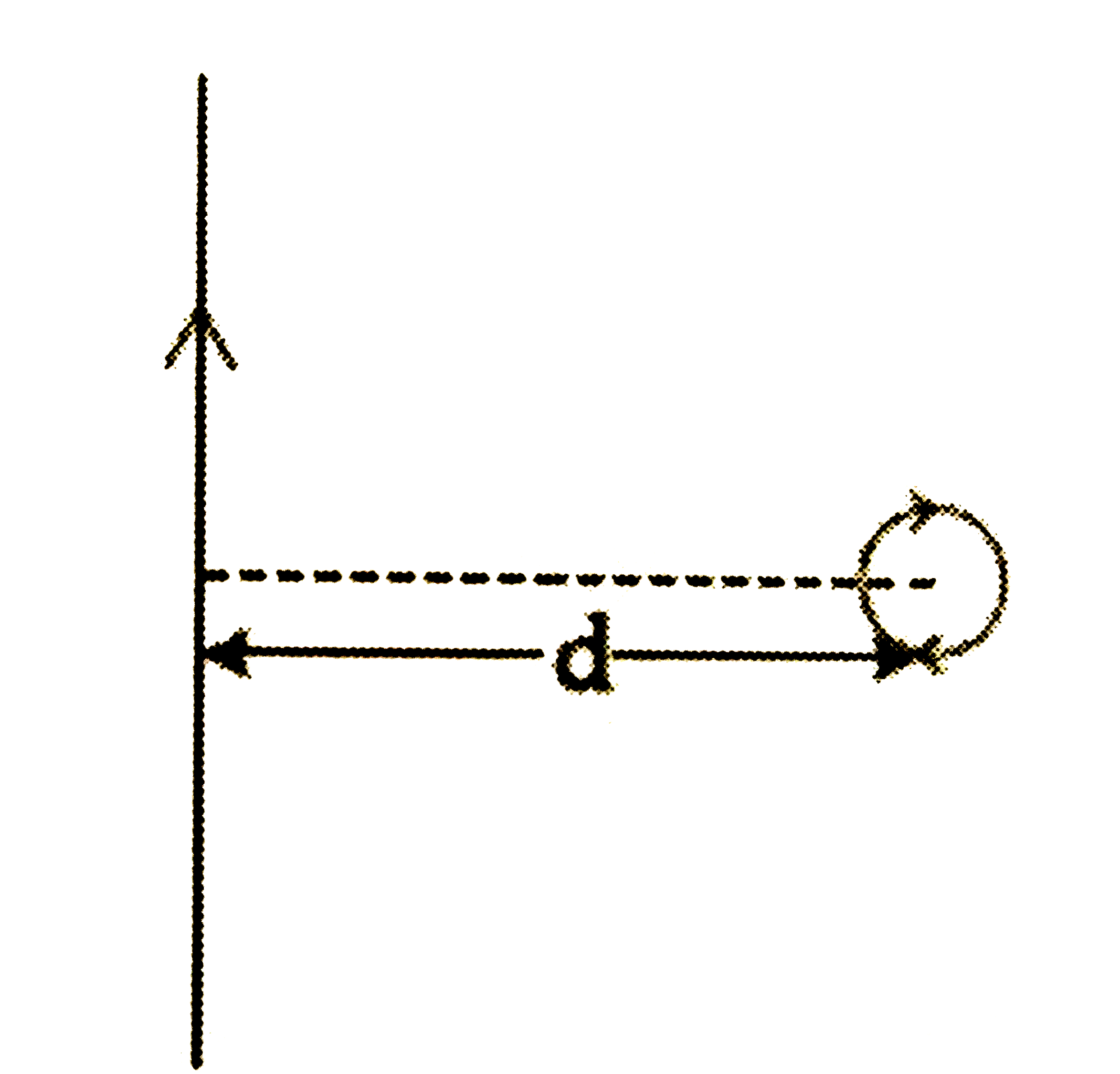
View Solution
Knowledge Check
A current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with x>0 is now bent so that it now lies in the y-z plane.
AThe magnitude of magnetic moment now diminishes.BThe magnetic moment does not change.CThe magnitude of →B at (0,0,z),z>>R increases.DThe magnitude of →B at (0,0,z),z>>R is unchanged.
A current carrying loop is free to turn in a uniform magnetic field. The loop will then come into equilibrium vhen its plane is inclined at
View SolutionAn infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its centre from the wire is d (d>>a). If the loop applies a force F on the wire then :

View SolutionAssertion If a magnet is brought closer to a current carrying loop along its axis, then current always decreases in the loop.
Reason Magnet is repelled by the loop.
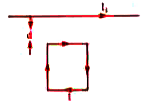
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance d from the donductor as shown in figure. The loop will experience
View SolutionA current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with x>0 is now bent so that it now lies in the y-z plane.
View SolutionA current − carrying circular loop of radius R is placed in the XY− plane with centre at the origin. Half of the loop with x>0 is now bent so that is now lies in the YZ− plane
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long staright conductor carryinf a steady current I, at a distance d from the conductor as shown in Fig. The loop wil experience
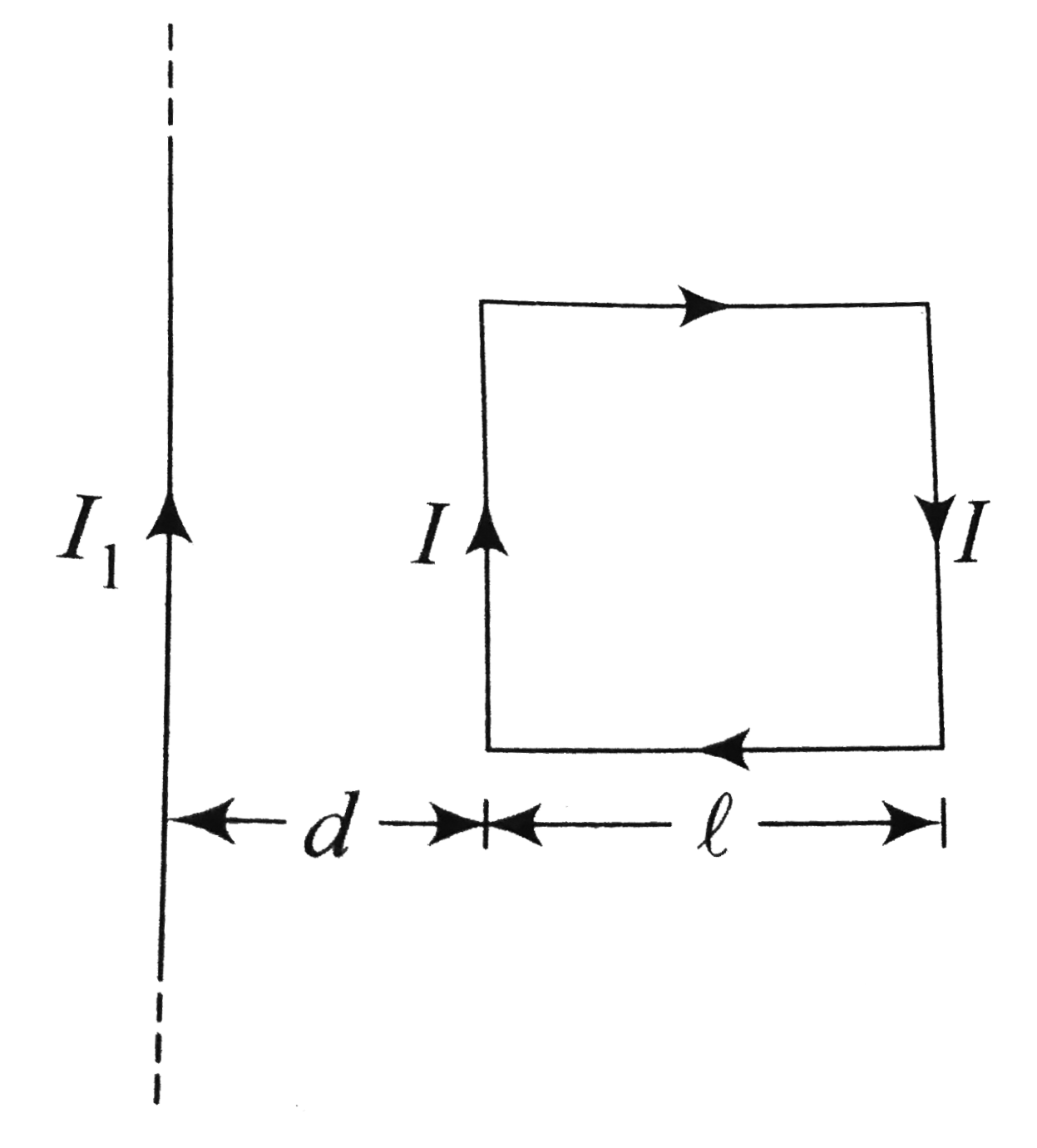
View Solution
