A current flowing through an infinite long wire divides between two infinite long wires and at junction B. The magnitude of the magnetic field at point O due to current through wires is :
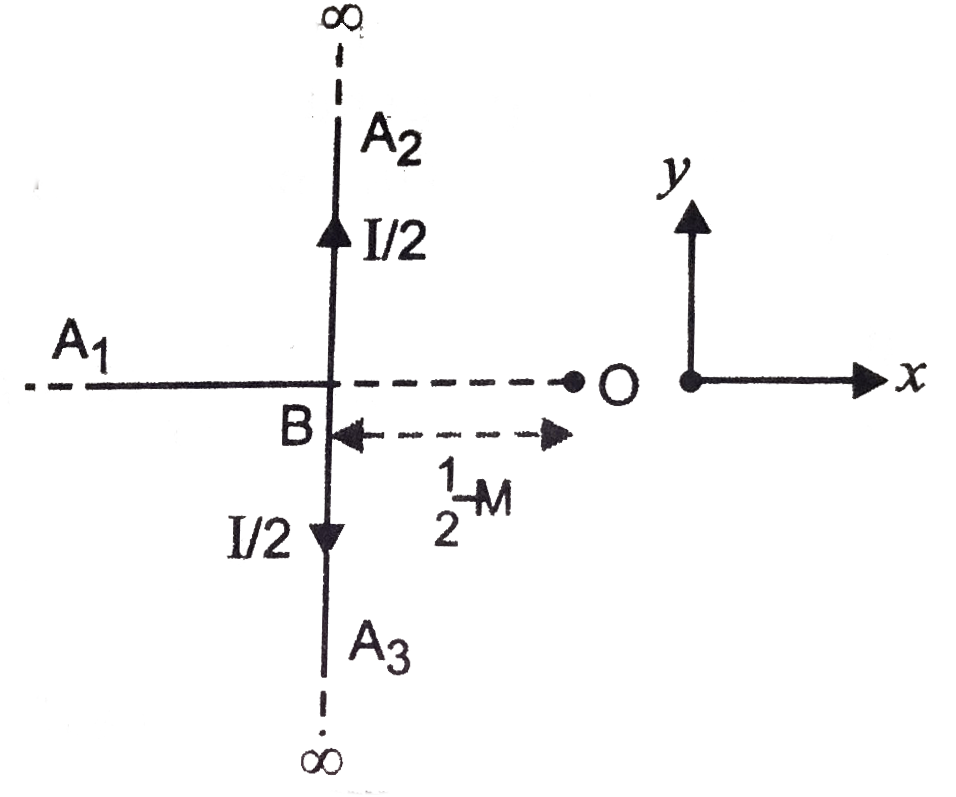
The correct Answer is:Zero
Let Mag. field at O due to current through wires
be and respectively. Then
OA_1B_2=(mu_0)/(4pi)(I)/((1//2))[sin 90^@+sin0^@](-hatk)=10^-7xx1xx2[1+0](-hatk)=-2xx10^-7hatkvecB_3=(mu_0)/(4pi)(I)/((1//2))[sin 90^@+sin 90^@]hatk=10^-7xx1xx2[0+1]hatk=2xx10^-7hatk:.vecB=vecB_1+vecB_2+vecB_3=0+(-2+10^-7hatk)+(2xx10^-7hatk)=0
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The magnetic field at the origin due to the current flowing in the wire is
 A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk)
A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk) - Question 2 - Select One
Two infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
ATwice the magnetic field produced due to each of the wiresBHalf of the magnetic field produced due to each of the wiresCSquare of the magnetic field produced due to each of the wiresDZero - Question 3 - Select One
Two infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
ASquare of the magnetic field produced due to each of the wiresBhalf of the magnetic field produced due to each of the wiresCtwice the magnetic field produced due to each of the wiresDzero
Two perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
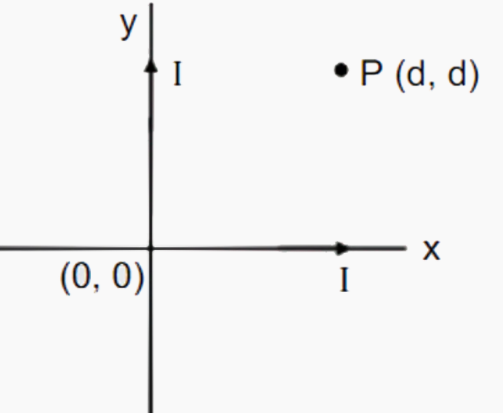 View Solution
View SolutionThe direction of magnetic field at a point due to an infinitely long wire carrying current is
View SolutionA current I flows an infinitely long wire with cross section in the form of a semi - circular ring of radius R. The magnitude of the magnetic induction along its axis is :
View SolutionTwo long thin wires ABC and DEF are arranged as shown in the figure. They carry currents I. The magnitude of the magnetic field at O is
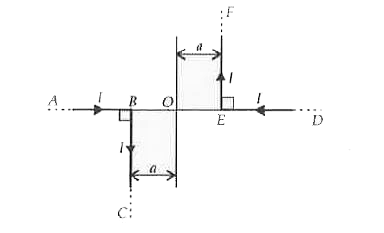 View Solution
View SolutionIf a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
View Solution


