A current source sends a current I=(i0)cos(ωt), When connected across an unknown load, it gives a voltages output of v=v0sin[ωt+(π/4)] across that load. Then the voltage across the current source may bebroaught in phase with the current through it by
![A current source sends a current I=(i0) cos (omegat), When connected across an unknown load, it gives a voltages output of v=v(0)sin [omega t+(pi//4)] across that load. Then the voltage across the current source may bebroaught in phase with the current through it by](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V05_C05_E01_083_Q01.png)
connecting an inductor in series with the load
connecting a capacitor in series with the load
connecting an inductor in parallel with the load
connecting a capacitor in parallel with the load.
The correct Answer is:C
Step by step video, text & image solution for A current source sends a current I=(i_0) cos (omegat), When connected across an unknown load, it gives a voltages output of v=v_(0)sin [omega t+(pi//4)] across that load. Then the voltage across the current source may bebroaught in phase with the current through it by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the question number 44, the phase difference between the voltage across the source and current is
A80.2∘B31∘C50.2∘D38.2∘The value of current in two series LCR circuits at resonance is same when connected across a sinusodial voltage source. Then:
Aboth circuits must be having same value of capacitance and inductorBin both circuits ratio of L and C will be sameCfor both the circuits XL/XC must be same at that frequencyDboth circuits must have same impedance at all frequenciesIf an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π)
If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
View SolutionAn ac source of voltage V=Vmsinωt is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is
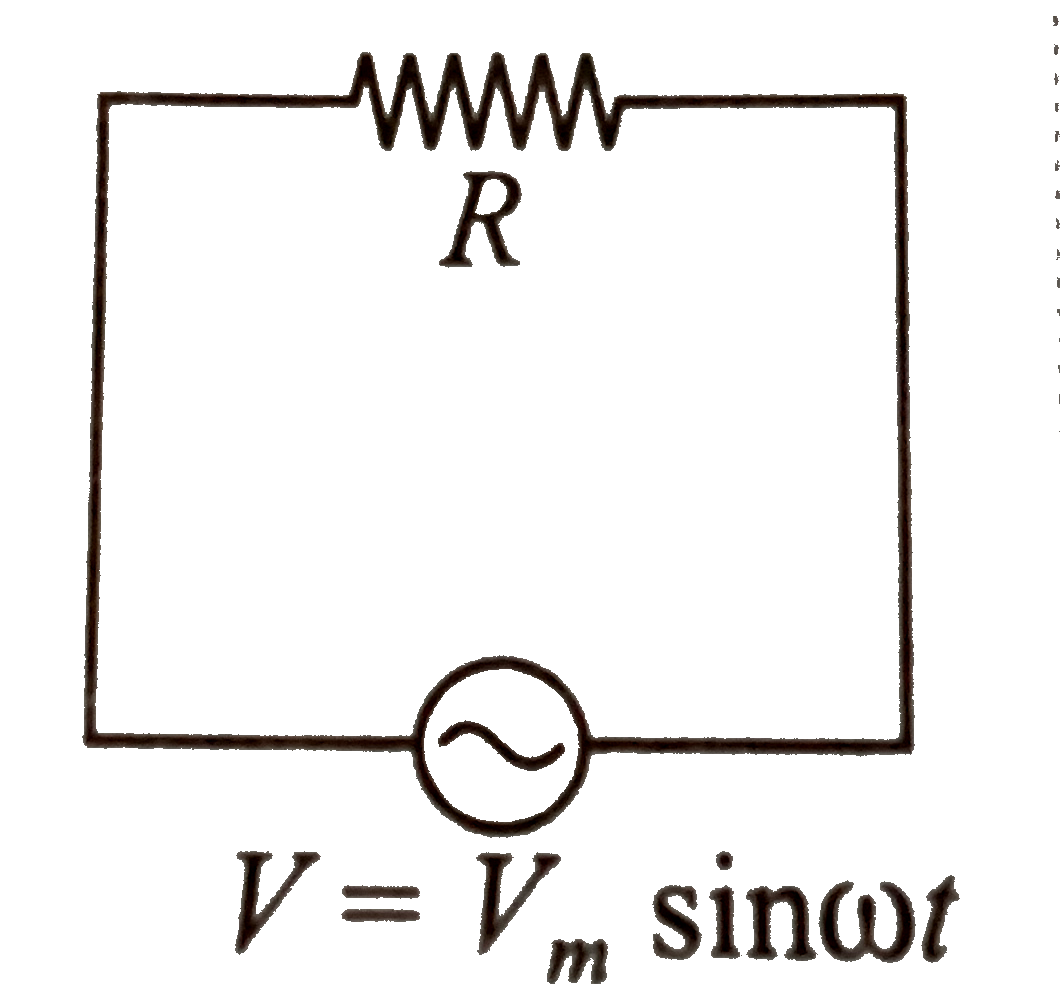
View SolutionAC source of voltage of V=V0sin(100t) is connected with box which contain ether RL of RC circuit. If voltage leads the current by phase π/4 then :
View SolutionWhen an alternating voltage of 220V is applied across a device P, a current of 0.25A flows through the circuit and it leads the applied voltage by a angle π2 radian. When the same voltage source is connected across another device Q, the same current is observed in the circuit but in phase with the applied voltage. What is the current when the same source is connected across a series combination of P and Q?
View SolutionAn alternative voltage V=10sinωt (in volts) is applied across a parallel arrangement as shown current (in A) through the source is best described by
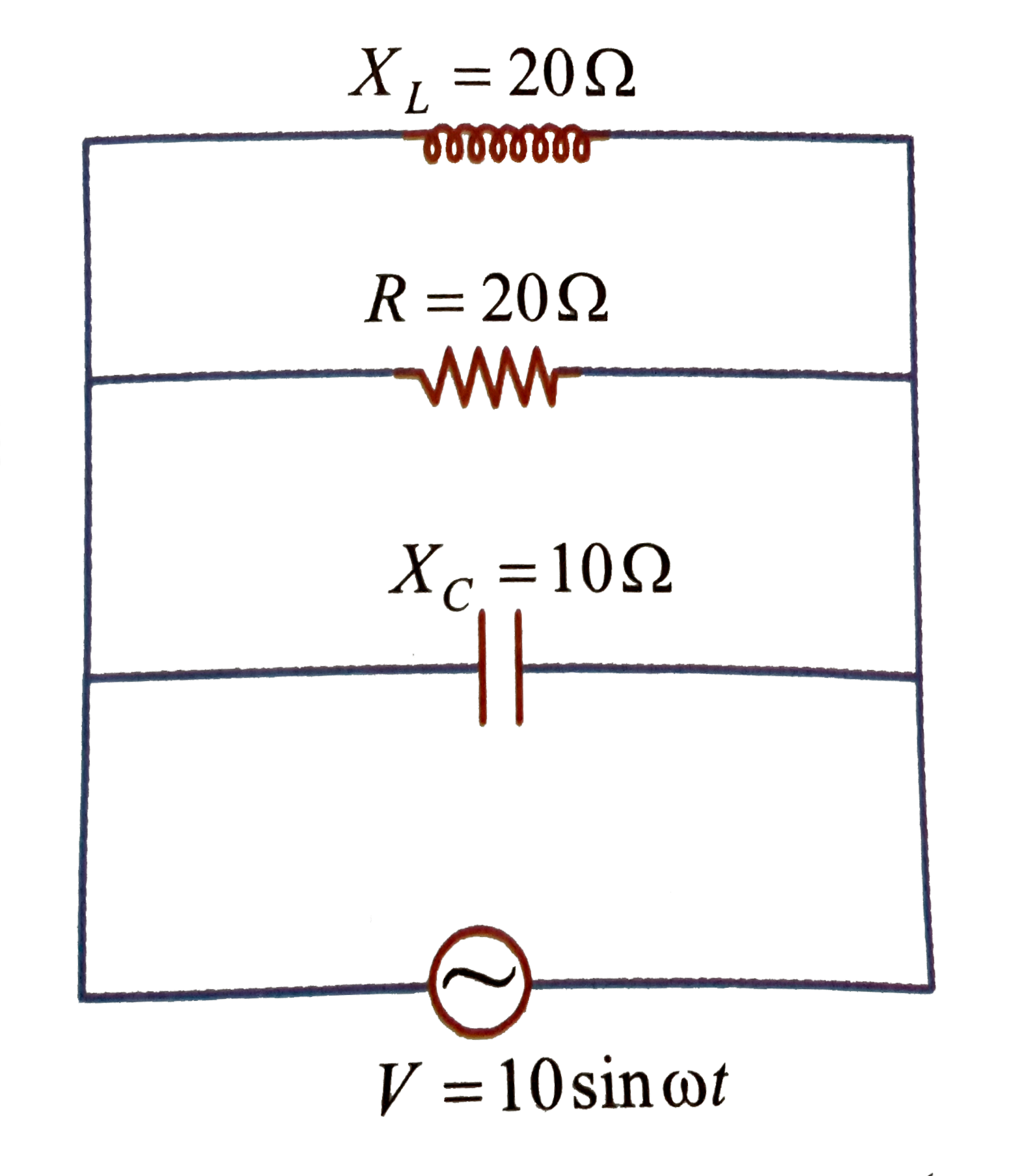
View Solution

