A cylinder is rotated clockwise and lowered slowly on arough inclined plane with (μ=0.8). Then:

cylinder will start going upwards
cylinder will start going downwards
frictional force will act upwards
frictional force will act downwards
The correct Answer is:B, C
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - COMPREHENSION_TYPE29videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE83videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
A disc is rotated about its axis with a certain angular velocity and lowered gently on a rough inclined plane as shown in Fig., then
 AIt will rotate at the position where it was placed and then will move downwardsBIt will go downwards just after it is loweredCIt will go downwards first and then climb upDIt will climb upwards and then move downwards
AIt will rotate at the position where it was placed and then will move downwardsBIt will go downwards just after it is loweredCIt will go downwards first and then climb upDIt will climb upwards and then move downwards - Question 2 - Select One or More
A solid cylinder is rolling down a rough inclined plane of inclination θ. Then
AThe friction force is dissipativeBThe friction force is necessarily changingCThe friction force will aid rotation but hinder translationDThe friction force is reduced if θ is reduced - Question 3 - Select One or More
A solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.
A solid cylinder is rolling down a rough inclined plane of inclination θ. Then
View SolutionA spinning cylinder of mass m and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
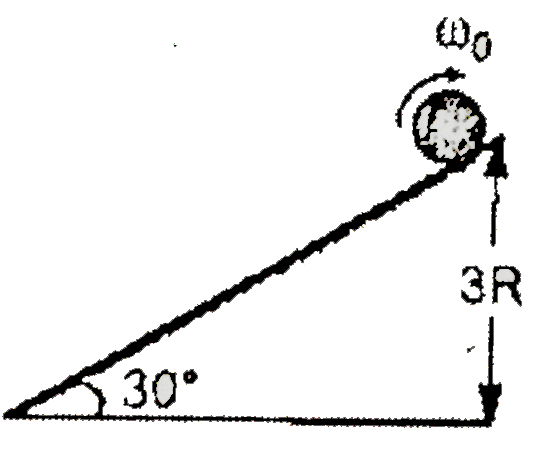 View Solution
View SolutionIf a solid cylinder rolls down an inclined plane, then its:
View SolutionAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
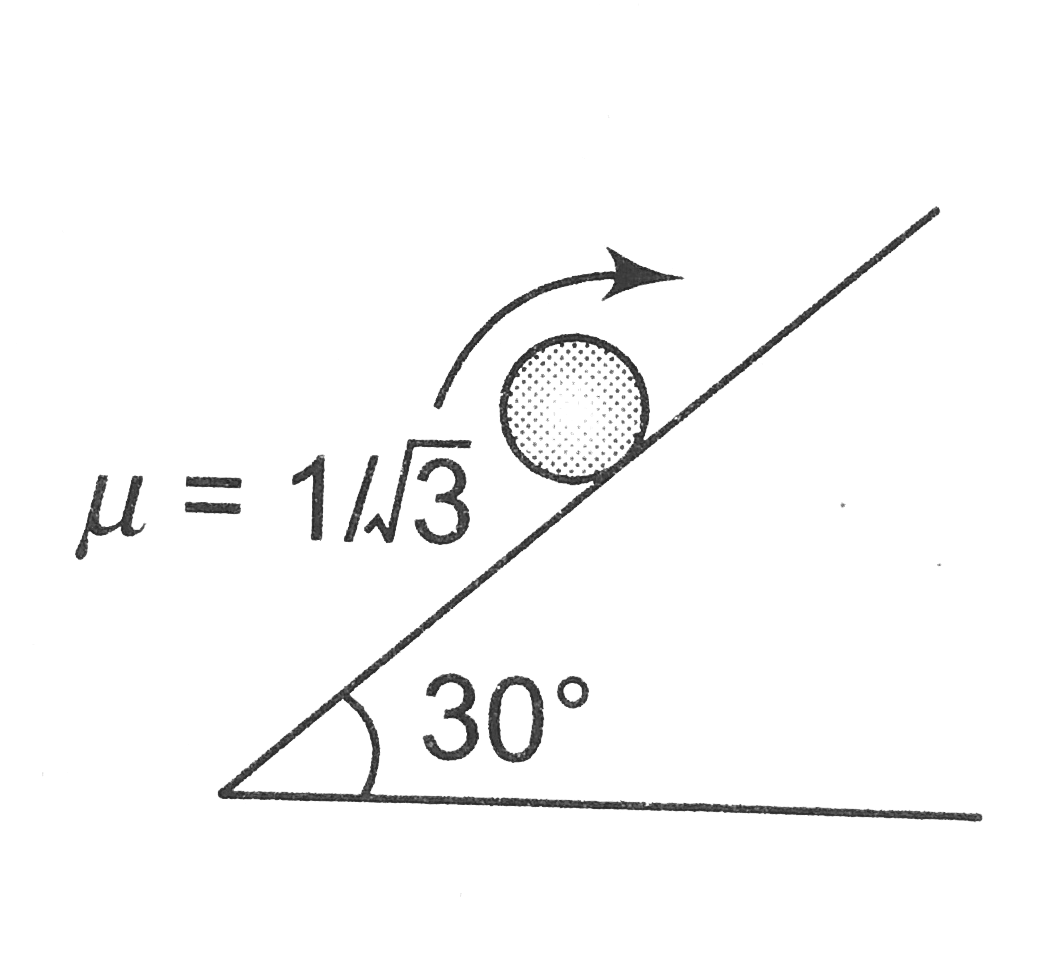 .View Solution
.View SolutionIf a solid cylinder rolls down an inclined plane, then its:
View Solution

