A cylinder of mass $m$ rolls without slipping on an inclined plane of inclination $θ$ . Find the liner acceleration of the sphere and friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?

Video Solution

Text Solution

Verified by Experts

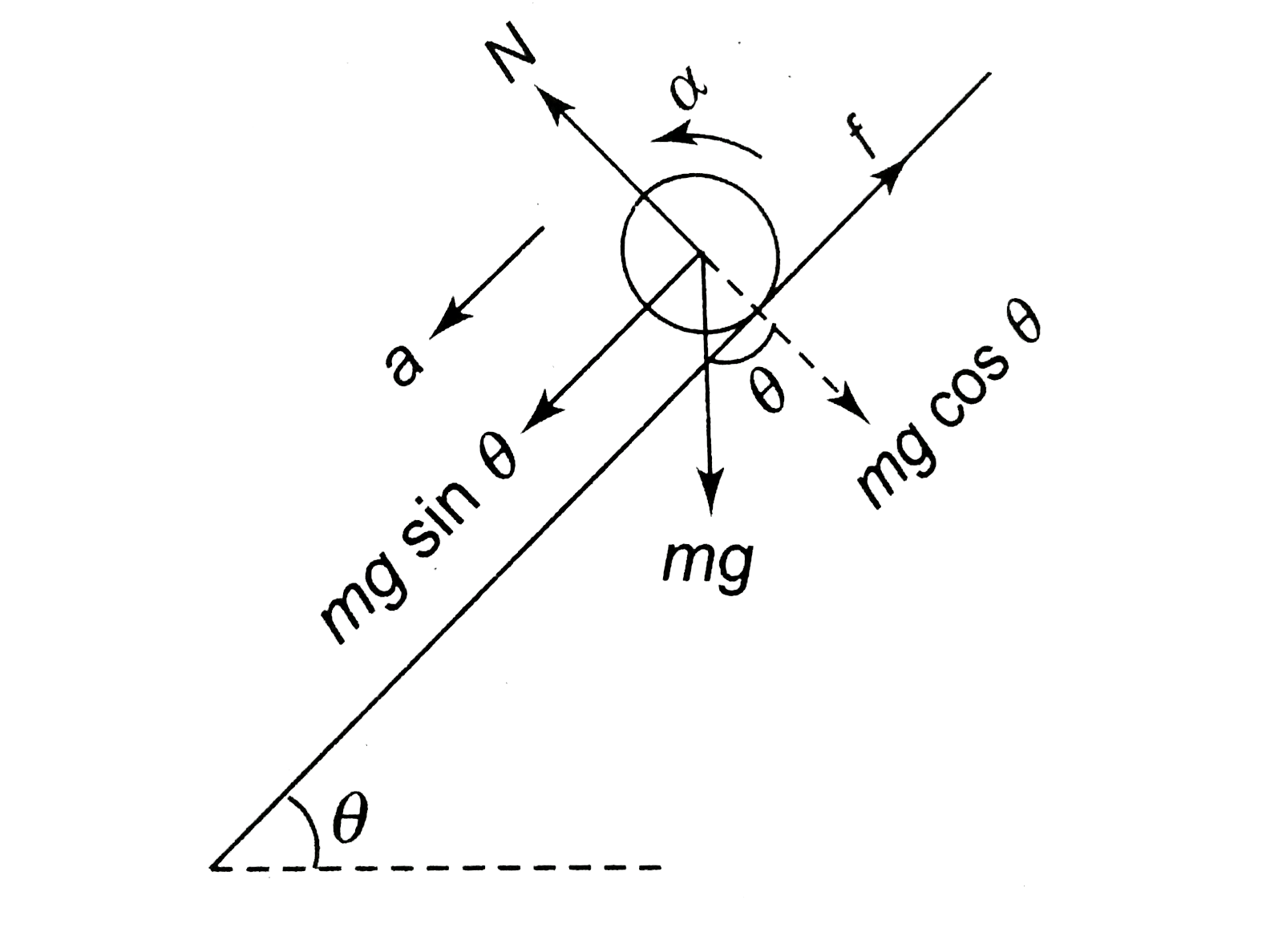
Linear motion: $m g sin θ - f = m a$ ( $i$ )
Rotational motion: $f R = I α = (\frac{1}{2} m r^{2}) (\frac{a}{r})$
$f = \frac{1}{2} m a$ ( $i i$ )
(for pure rolling $a = r α$ )
From ( $i$ ) and ( $i i$ )
$m g sin θ - \frac{1}{2} m a = m a$
$m g sin θ = \frac{3}{2} m a \Rightarrow a = \frac{2}{3} g sin θ$
$f = \frac{1}{2} m a = \frac{1}{3} m g sin θ$
$f_{max} = μ N = μ m g cos θ :$ coefficient of static friction.
For pure rolling $f_{max} \geq f$
$μ m g cos θ \geq \frac{1}{3} m g sin θ \Rightarrow μ \geq \frac{1}{3} tan θ$
$μ_{min} = \frac{1}{3} tan θ$
OR
In pure rolling
$a = \frac{g sin θ}{1 + k^{2} / R^{2}} = \frac{g sin θ}{1 + \frac{1}{2}} = \frac{2}{3} g sin θ$
$m g sin θ - f = m a \Rightarrow f = \frac{1}{3} m g sin θ$
$μ \geq \frac{tan θ}{1 + \frac{R^{2}}{k^{2}}}$
$μ_{min} = \frac{tan θ}{1 + 2} = \frac{1}{3} tan θ$

Updated on:21/07/2023