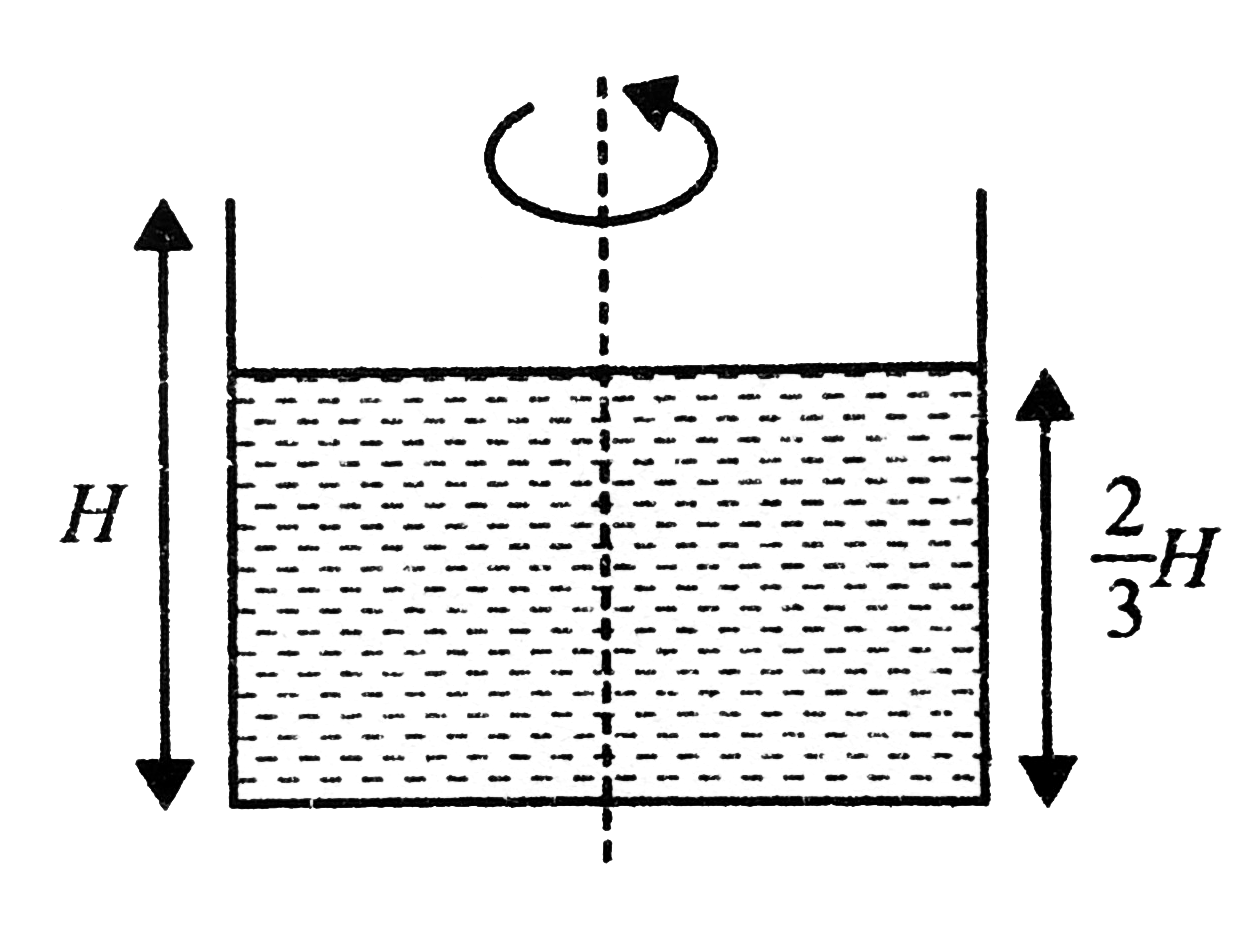
A cylinder of radius R and height H is foam unknown height h. When is rotated at an unknown constant angular velocity ω, the base of the cylinder gets exposed when the liquid just starts spilling out, as shown in Fig.
a. Find the height h of the liquid.
b. Find the angular speed w of the cylinder.

Since the original level of water before rotation is equal to the average of the minimum and maximm water level after rotation, therefore
h=+H2
b. The equation of the parabolic surface is
y=ω2r22g (∴y0=0)
We know that for r=R,y=H, thus
H=ω2R22g or ω=√(2gH)R
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.3
10 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Let the area of the base of a cylinder be B and the height of the cylinder be h. Write a formula for the cylinder’s volume V.
View SolutionA cylinder of radius R=1m and height H=3m two- thirds filled with water, is rotated about its vertical axis as shown in Fig. Determine the speed of rotation when
a. the: water just starts spilling over the rim.
b. the point at the centre of the base is just exposed.

View Solution
Knowledge Check
A circular cylinder of radius R and height H is filled with water to a height (2/3)H. It starts rotating about its axis with constantly increasing angular speed. Choose the correct alternatives.
 AAt all speeds, shape of the free surface is parabolloid.BThe free surface touches first the brim of the cylinder and then the base of the cylinder.CThe free surface cannot touch the base without spilling water.DThe free surface touches the brim as well as the base at the same instant.
AAt all speeds, shape of the free surface is parabolloid.BThe free surface touches first the brim of the cylinder and then the base of the cylinder.CThe free surface cannot touch the base without spilling water.DThe free surface touches the brim as well as the base at the same instant.A solid cylinder of radius r and height h is melted and casted into a cone. If radius of cone is (r2) then find its height.
A4 hB6 hC12 hD8 h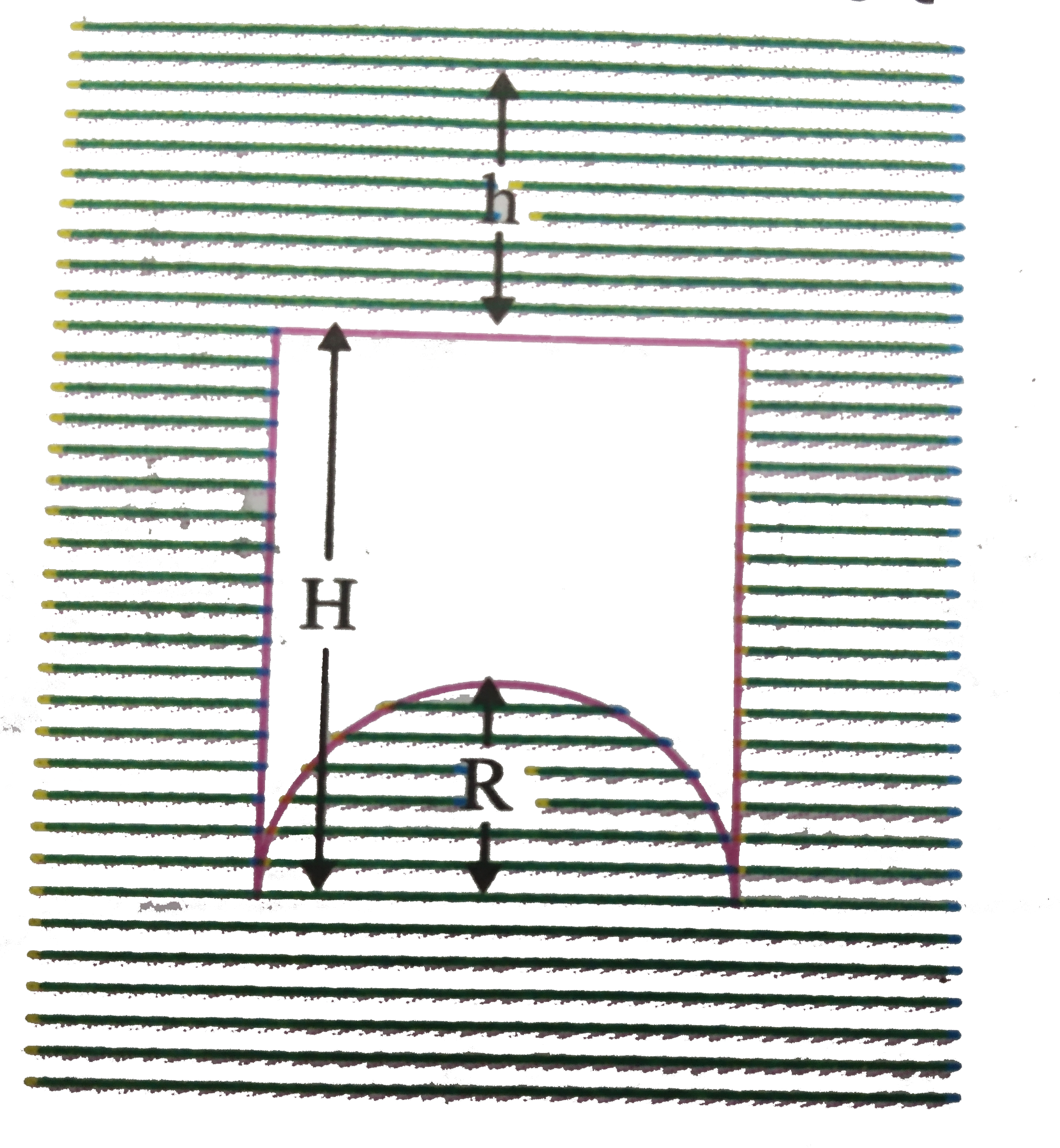
A cylinder of radius R, height H and density simga has a hemispherical cut at its bottom. The top of the cyliner is kept at depth h from the liquid surface. If the density of liquid is ρ, find the hydrostatic force acting on the hemispherical surface of the cylinder.AF2=πR2ρg(H+h−23R)BF2=πR2ρg(H−h+23R)CF2=πR2ρg(H−h−23R)DF2=πR2ρg(H+h+23R)
Radius of a cylinder is r and the height is h. Find the change in the volume if the
height is doubled.
View SolutionA long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
View SolutionFrom a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
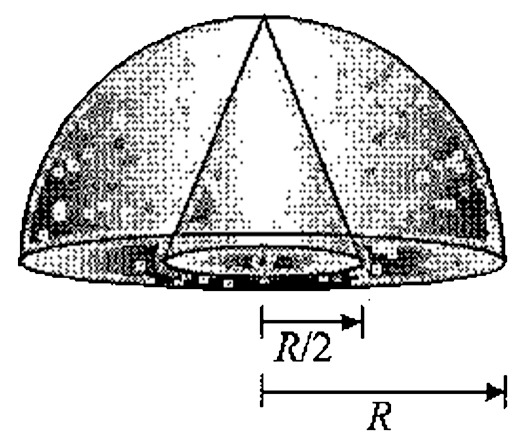
View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View Solution
