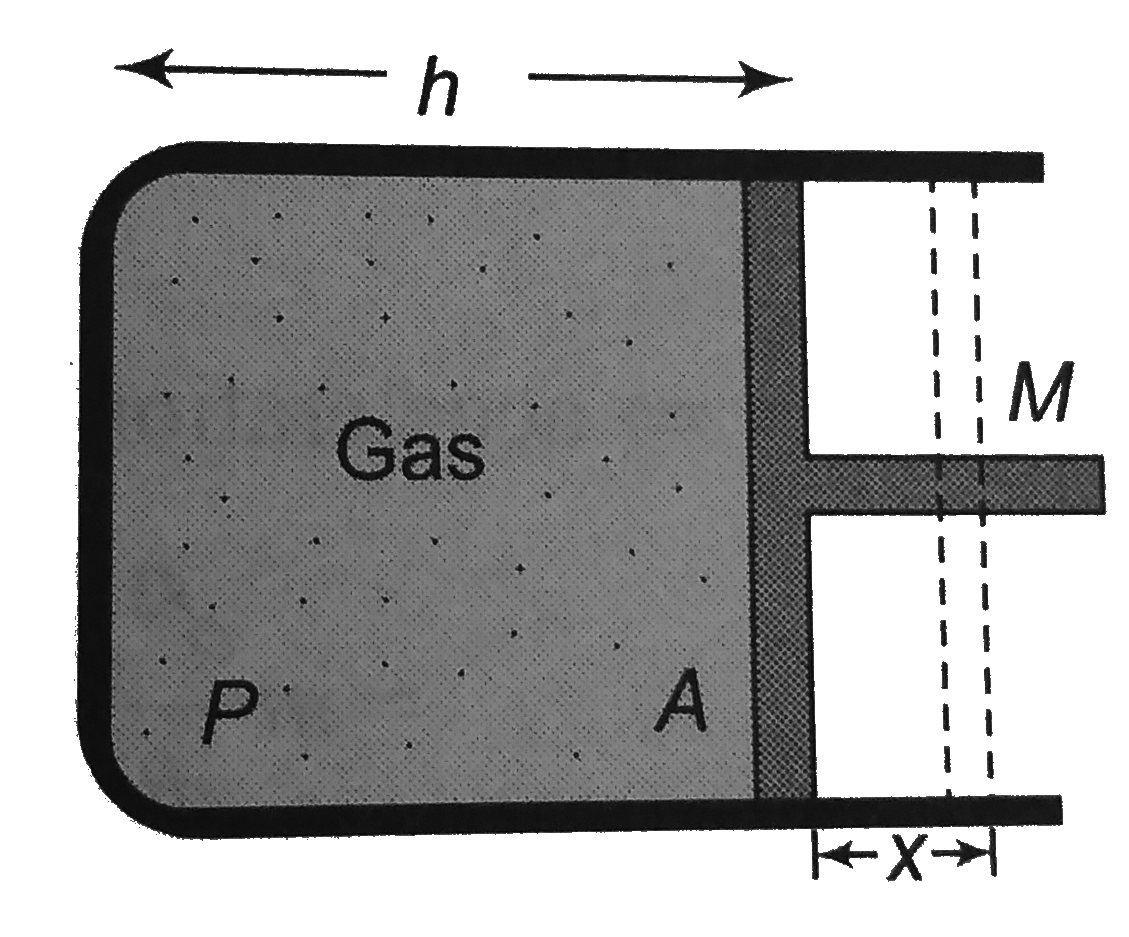
A cylinder piston of mass M sides smoothly inside a long cylinder closed at and enclosing a certain mass of gas The cylinder is kept with its axis horizontal if the piston is distanced from its equations positions it oscillation simple harmonically .The period of oscillation will be

T=2π√(MhPA)
T=2π√(MAPb)
T=2π√(MPAh)
T=2π√MPhA
The correct Answer is:A
Let the piston be displace through distance x toward left then velocity drcrease pressed increase if pressure and ΔV is decrerase in volume then considring the pracess as take place gravity (i.e.sothermal)
P1V1=P2V2⇒PV(P+Δp)(V−ΔV)
⇒PV=PV+ΔPV−ΔPΔV
⇒ΔP.V−P(Ah)=P(Ax)⇒ΔP(Ax)⇒ΔP=P.xh
This execute pressed is responsible the reastroing force (F) to the pistom of mass M
Hence F=ΔpA=pksh
comparing a with (F)=kx⇒k=Mω2=pAh
⇒ω=√pAMh⇒T=2π√MhpA
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - AIIMS Questions24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
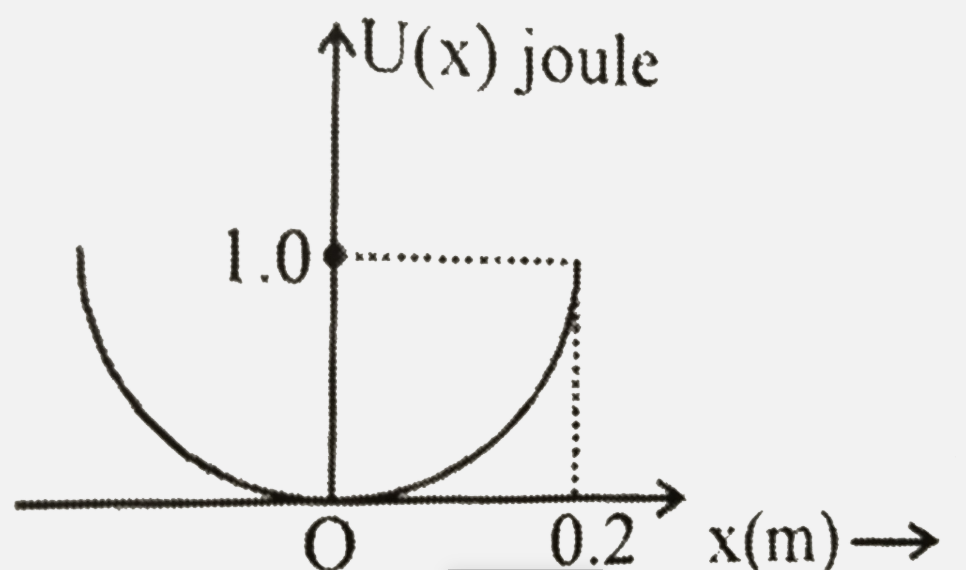
A particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
 View Solution
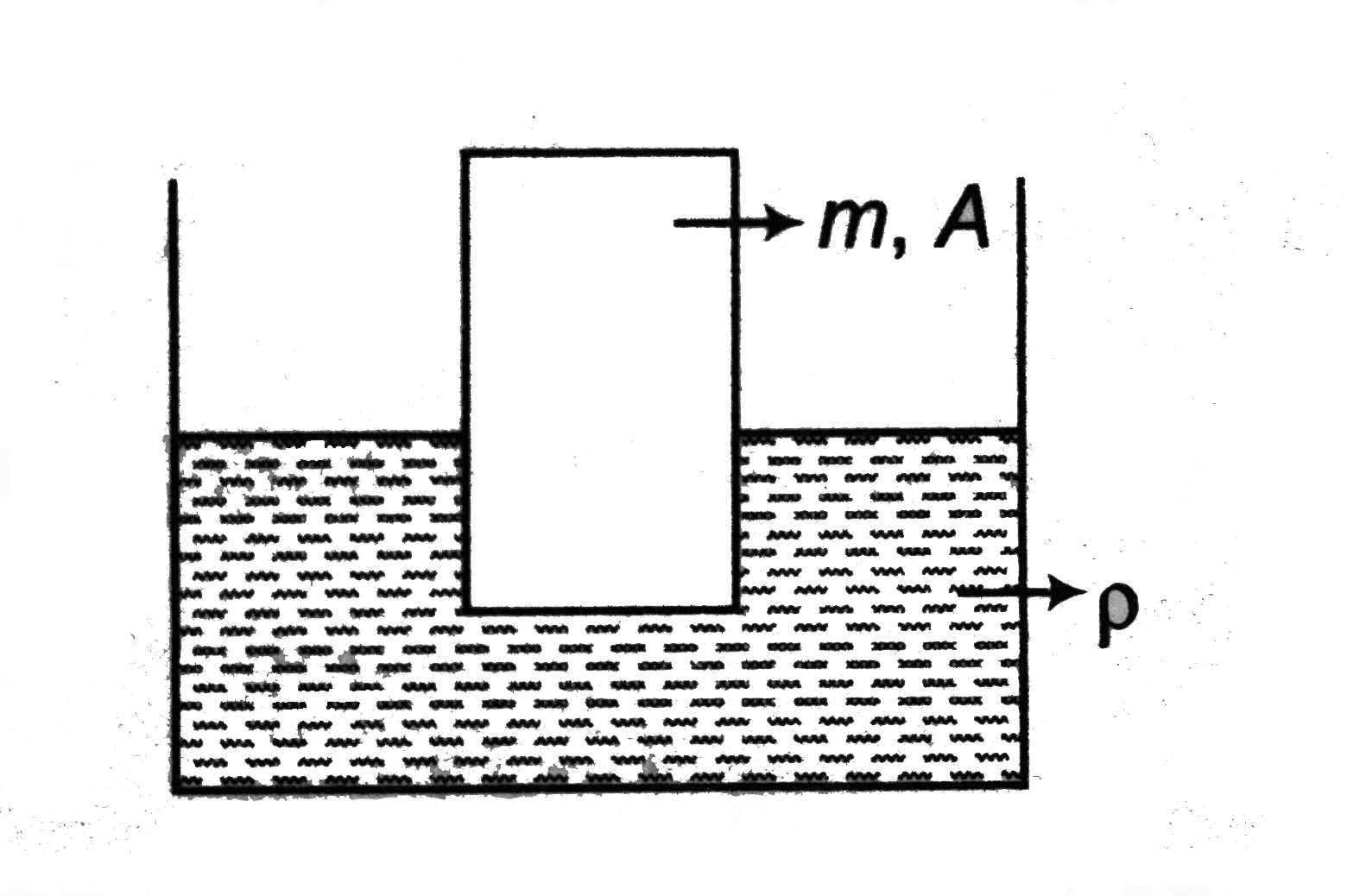
View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical piston of mass M slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of gas. The cylinder is kept with its axis horizontal. If the piston is disturbed from its equilibrium position, it oscillates simple harmonically. Pressure inside the gas in equilibrium is P. Consider the piston to be diathermic so that process is isothermal the period of oscillation will be:
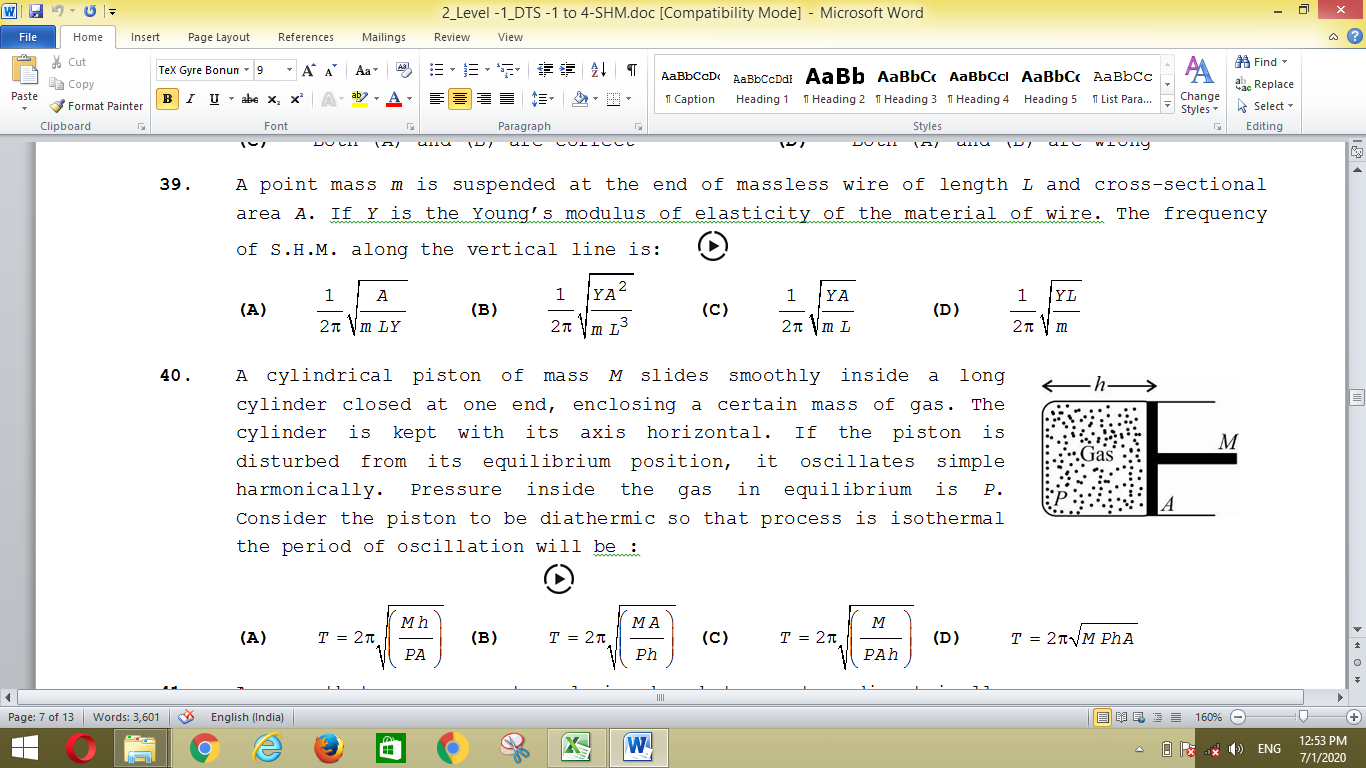 AT=2π√(MhPA)BT=2π√(MAPh)CT=2π√(MPAh)DT=2π√MPhA
AT=2π√(MhPA)BT=2π√(MAPh)CT=2π√(MPAh)DT=2π√MPhA - Question 2 - Select One
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
 A2π5sB2√2π5sC√2π5sD4π5s
A2π5sB2√2π5sC√2π5sD4π5s - Question 3 - Select One
The moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
A12M(a2+2b2)B12M(2a2+b2)C12M(a2+b2)D12M(a23+b212)
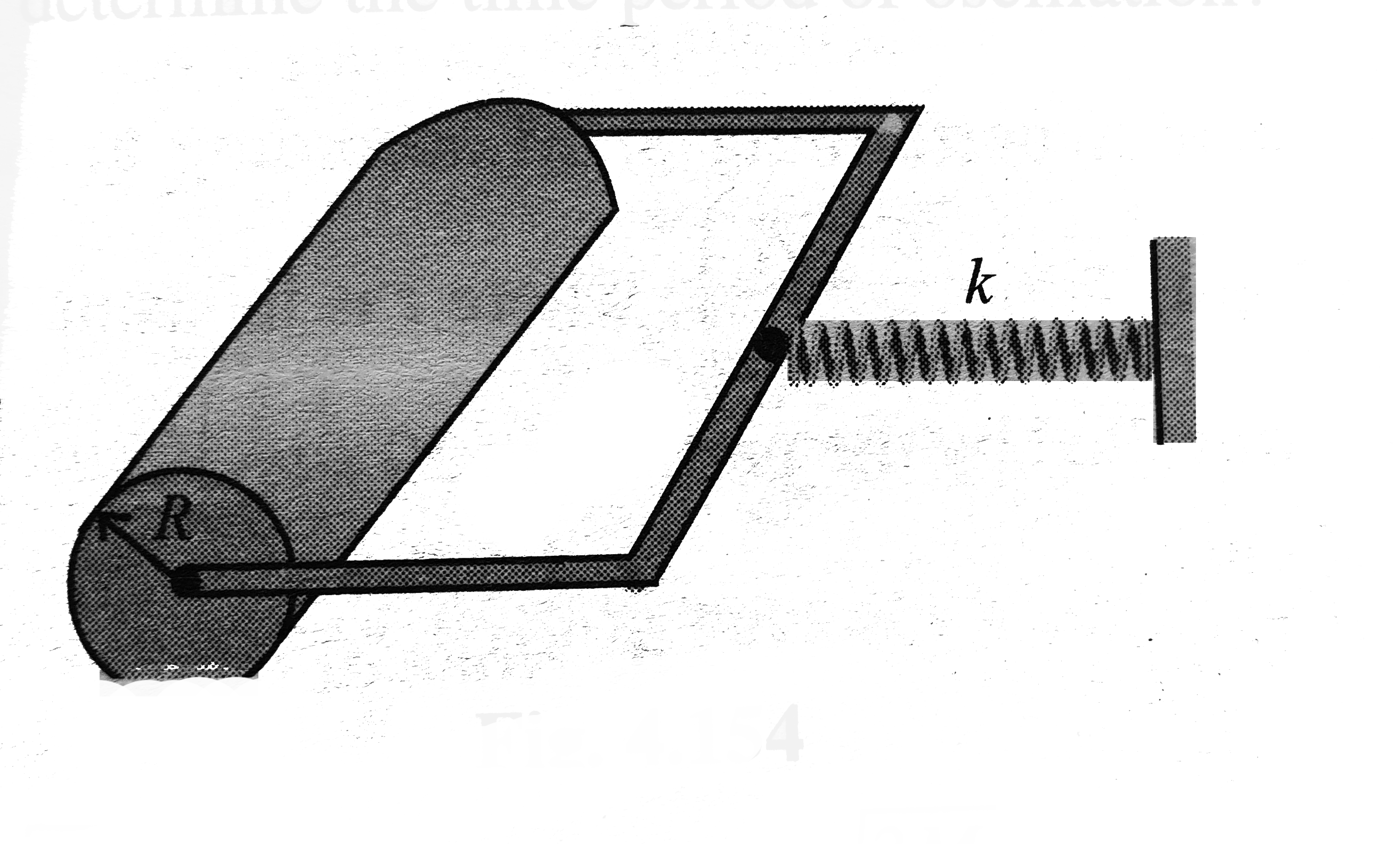
A soil cylinder of mass M and radius R is connected to a spring as shown in fig. The cylinder is placed on a rough horizontal surface. All the parts except the cylinder shown in the figure are light. If the cylinder is displaced slightly from its mean position and released, so that it performs pure rolling back and forth about its equilibrium position, determine the time period of oscillation?View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.
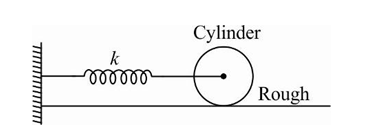
At a distance x1 from the equilibrium position, kinetic energy of the oscillating system becomes equal to potential energy then, x1is equal to:View SolutionThe acceleration of a simple harmonic oscillator is 1m/s2 when its displacement from mean position is 0.5 m. Then its frequency of oscillation is
View SolutionA ideal gas is kept in a cylinder of cross sectional area A and volume v0. The mass of the gas enclosed is M and bulk modulus B. If the piston of the cylinder is pressed by small x, then find the time period of small oscillations,
View Solution

