A cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω, the cylinder falls off the disc, if the distance between the axes of the disc and cylinder is R, and the coefficient of friction μ>D/h where D is the diameter of the cylinder and It is its height.

The correct Answer is:√DhR
The centripetal force that keeps the cylinder at rest on the disc is the frictioal force f. According to a non inertial observer on disc a pseudo force the cylinder reacts with an equal and oppostite force, F, which sometimes is reffered to as the centrifugal force.

F=mω2R
where M is the mass of the cylinder.
The cylinder can fall off either by slipping away or by tilting about point P, depending of whichever takes place first. the critical agular speed w1 for slipping occurs when F equals f:F=f
Mω21R+μgM
where g is the gravitational acceleration. Hence ω1=√μgR
F ties to rotaste the cylinder about P, but the weight W opposes it. The rotatiion becomes pssible, when the torque caused by W.
Fh2=WD2⇒F=WDh
Mω22R=MgDh
giving ω2=√DhR
Since we are given μ>Dh, we see that ω1>ω2 and the cylinder falls off by rolling over at ω=ω2.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct
97 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.4
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A coin placed on a horizontal rotating disc, with its centre at 10 cm from the centre of the disc, is about to slip off when the disc performs 60 rpm. Find the coefficient of friction between the coin and the disc.
View SolutionA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
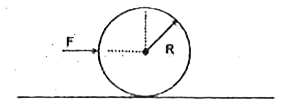
View Solution
Knowledge Check
A force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
 Ain the direction of FBzeroCin opposite direction of FDcan not be ascertained
Ain the direction of FBzeroCin opposite direction of FDcan not be ascertainedAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
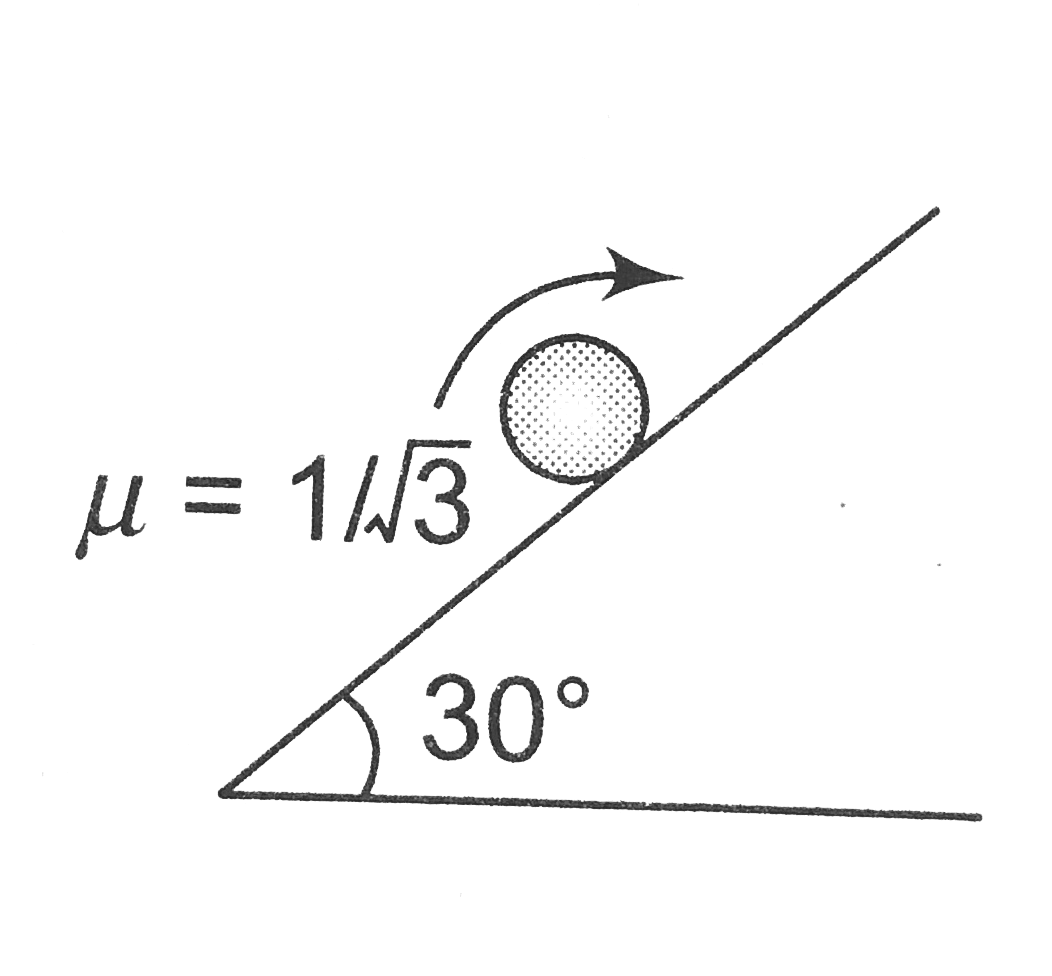 .Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
.Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
Two discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then
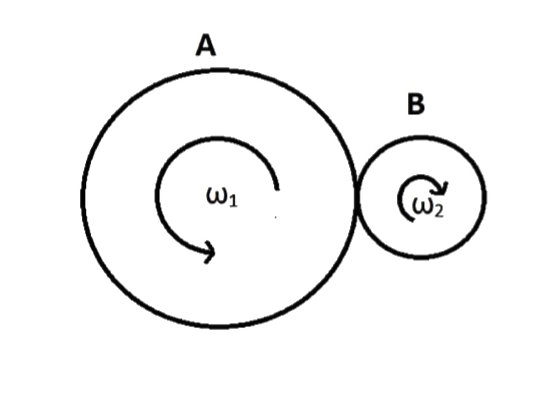
View SolutionTwo discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then

View SolutionSelect ALL correct answer :
A disc of radius R is placed over a horizontal table in such a way that plane of the disc is horizontal and rotated about its vertical axis passing through its center with angular velocity ω. A layer of grease of thickness l is present between the table and the disc.Coefficient of viscosity of grease is η .Then,
(A) torque needed to rotate the disc with constant angular velocity is πηωR44l
(B) torque needed to rotate the disc with constant angular velocity is πηωR42l
(C) power needed to rotate the disc with constant angular velocity is πηω2R42l
(D) power needed to rotate the disc with constant angular velocity is πnω2R44l
View SolutionA uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity ω0, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to μ. Find
(a) how long the cylinder will move with sliding,
(b) the total work performed by the sliding friction force acting on the cylinder.
View SolutionA cylinder of radius R and height H is foam unknown height h. When is rotated at an unknown constant angular velocity ω, the base of the cylinder gets exposed when the liquid just starts spilling out, as shown in Fig.
a. Find the height h of the liquid.
b. Find the angular speed w of the cylinder.

View SolutionA cylinder of radius R and height H is foam unknown height h. When is rotated at an unknown constant angular velocity ω, the base of the cylinder gets exposed when the liquid just starts spilling out, as shown in Fig.
a. Find the height h of the liquid.
b. Find the angular speed w of the cylinder.

View Solution
