A cylindrical aluminium rod, with an initial length of 0.8000 m and radius 1000.0 μm, is clamped in place at one end and then stretched by a machine pulling parallel to its length at its other end. Assuming that the rod's density (mass per unit volume) does not change, find the force magnitude that is required of the machine to decrease the radius to 999.9μm (The yield strength is not exceeded, Ealuminium=70×109N/m2).
The correct Answer is:44
To solve the problem step by step, we will use the concepts of elasticity, specifically Young's modulus, and the relationship between stress, strain, and force.
Step 1: Understand the problem and gather the given data
- Initial length of the rod, L0=0.8000m
- Initial radius of the rod, R0=1000.0μm=1000.0×10−6m
- Final radius of the rod, Rf=999.9μm=999.9×10−6m
- Young's modulus for aluminum, E=70×109N/m2
Step 2: Calculate the initial and final cross-sectional areas
The cross-sectional area A of a cylinder is given by the formula:
A=πR2
- Initial area A0:
A0=π(R0)2=π(1000×10−6)2=π(10−3)2=π×10−6m2
- Final area Af:
Af=π(Rf)2=π(999.9×10−6)2=π(999.92×10−12)m2
Step 3: Use the principle of conservation of volume
Since the density does not change, the volume before and after stretching must be equal:
A0L0=AfLf
Where Lf is the final length of the rod after stretching. Rearranging gives:
Lf=A0L0Af
Step 4: Calculate the change in length
The change in length ΔL is given by:
ΔL=Lf−L0
Step 5: Relate stress, strain, and Young's modulus
The stress σ is defined as:
σ=FA0
The strain ϵ is defined as:
ϵ=ΔLL0
According to Young's modulus:
E=σϵ
Thus:
F=σA0=E⋅ϵ⋅A0
Step 6: Substitute the values
Substituting for stress and strain:
F=E⋅(ΔLL0)⋅A0
Step 7: Calculate the force
Now we can calculate the force F using the values we have.
1. Calculate A0 and Af:
- A0=π(1000×10−6)2
- Af=π(999.9×10−6)2
2. Calculate Lf using the conservation of volume.
3. Calculate ΔL.
4. Substitute into the force equation to find F.
Final Calculation
After performing the calculations, we find:
F≈44N
- Initial length of the rod, L0=0.8000m
- Initial radius of the rod, R0=1000.0μm=1000.0×10−6m
- Final radius of the rod, Rf=999.9μm=999.9×10−6m
- Young's modulus for aluminum, E=70×109N/m2
The cross-sectional area A of a cylinder is given by the formula:
A=πR2
- Initial area A0:
A0=π(R0)2=π(1000×10−6)2=π(10−3)2=π×10−6m2
- Final area Af:
Af=π(Rf)2=π(999.9×10−6)2=π(999.92×10−12)m2
Since the density does not change, the volume before and after stretching must be equal:
A0L0=AfLf
Where Lf is the final length of the rod after stretching. Rearranging gives:
Lf=A0L0Af
The change in length ΔL is given by:
ΔL=Lf−L0
The stress σ is defined as:
σ=FA0
The strain ϵ is defined as:
ϵ=ΔLL0
According to Young's modulus:
E=σϵ
Thus:
F=σA0=E⋅ϵ⋅A0
Substituting for stress and strain:
F=E⋅(ΔLL0)⋅A0
Now we can calculate the force F using the values we have.
- A0=π(1000×10−6)2
- Af=π(999.9×10−6)2
After performing the calculations, we find:
F≈44N
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Matrix - Match)5videos
ELASTICITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)3videos
CURRENT AND RESISTANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )3videos
ELECTRIC CHARGES AND FIELDS
Similar Questions
A wire of length L is fixed at both ends such that F is tension in it. Its mass per unit length varies from one end to other end as μ=μ0x, where μ0 is constant. Find time taken by a transverse pulse to move from lighter end to its mid point.
View SolutionA thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View Solution
Knowledge Check
- Question 1 - Select One
A wire of length L and radius r is clamped at one end. On stretching the other end of the wire with a force F, the increase in its length is l. If another wire of same material but of length 2L and radius 2r is stretched with a force 2F, the increase in its length will be
Al4Bl2ClD2l - Question 2 - Select One
In the figure shown, the spring are connected to the rod at one end and at the midpoint. The rod is hinged at its lower end. Rotational SHM of the rod (Mass m, length L) will occur only if-
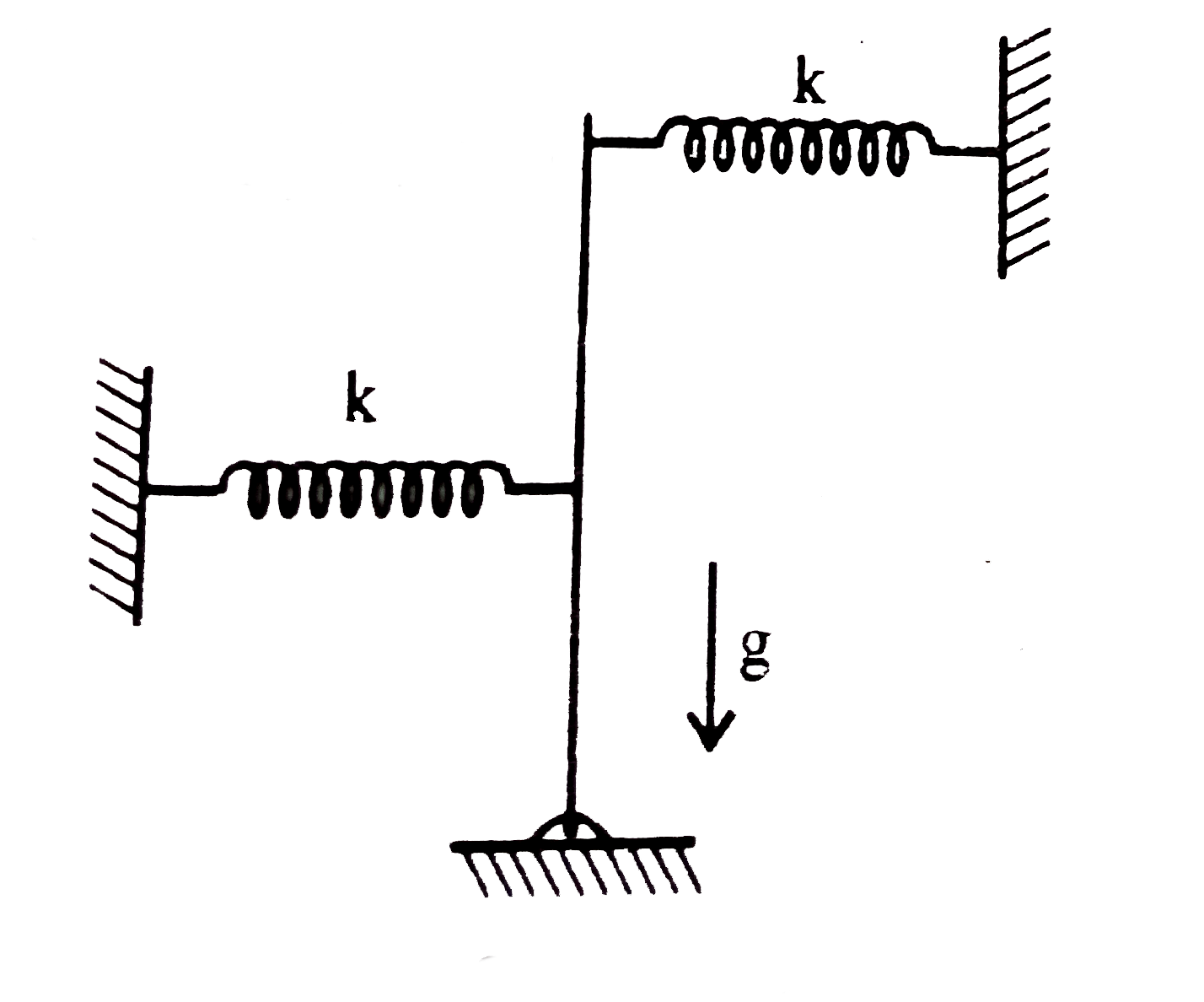Ak>mg/3LBk>2mg/3LCk>2mg/5LDk=0 - Question 3 - Select One
A steel rod of length 1 m and radius 10 mm is stretched by a force 100 kN along its length. The stress produced in the rod is YSteel=2×1011Nm−2
A3.18×106Nm−2B3.18×107Nm−2C3.18×108Nm−2D3.18×109Nm−2
A metallic wire of length 1 m is stretched to duble its length. Calculate the ratio of its initial and final resistances assuming that there is no change in its density on stretching.
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionFind radius of gyration of a rod of length l and mass m about an axis perpendicular its length through one end.
View SolutionA thin cylindrical rod of length 2.5m and radius 5mm is firmly fixed at upper end when lower end is twiced, the shear angle is found to be 0.06∘ then angle of twising is
View SolutionIf the linear density (mass per unit length) of a rod of length 3m is proportional to x, where x, where x is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is.
View Solution