A device called a toroid (figure) is often used to create an almost uniform magetic fiedl in some enclosed area. The device consists of a conducting wire wraped around a ring (a torus) made of a non conducting material. For a toroid having N closely spaced turns of wire, calculate the magnetic field in the region occupied by the torus, a distasnce r from the centre.
To calculate this field we must evaluate ∮B.dI over the circle of radius r. By symmetry we see that the magnitude of the field is constant on this circle and tangent to it.
so, ∮B.dI=Bl=B(2πr) 
Furthermore, the circular closed path surrounds N loops of wire each of which carries a current i . Therefore, right side of Eq. i is μ0Ni in this case
∴∮B.dI=μ0inet
or B(2πr)=μ0Ni
or B=μ0Ni2πr
this result shows that B∝1r
and hence is non uniform in the region occupied by torus. However, if r is very large compared with the cross sectional radius of the torus, then the field is approximately uniform inside the torus.In that case 
N2πr=n=number of turns per unit length of torus
∴B=μ0ni
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:Exercise
Explore 160 Videos
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
(a) Find magnetic field inside a long solenoid, carrying current (1/π) A and having number of turns per unit length 10. Also calculate magnetic field at ends.
(b) A long solenoid is fabricated by closely winding a wire of diameter 10mm over a cylinderical non-magnetic frame so that the successive turns nearly touch each other. Find magnetic field at the centre and ends of solenoid if it carriers a current (4/π) A?
(c) A single-layer coil (solenoid) has length l and cross-section radius R. The number of turns per unit length is equal to n. Find the magnetic induction at the centre of the coil when a current i flows through it.
(d) A solenoid of length 0.4m and diameter 0.6m consists of a single layer of 1000 turns of the fine wire carrying a current of 5mA. Calculate the magnetic field on the axis at the middle and at the ends of the solenoid.
View SolutionIII. Read the following text and answer the following questions on the basis of the same:
TOROID
A toroid is a coil of insulated or enamelled wire wound on a donut-shaped form made of powdered iron. A toroid is used as an inductor in electronic circuits, especially at low frequencies where comparatively large inductances are necessary.
A toroid has more inductance, for a given number of turns, than a solenoid with a core of the same material and similar size. This makes it possible to construct high-inductance coils of reasonable physical size and mass. Toroidal coils of a given inductance can carry more current than solenoidal coils of similar size, because large-diameter wires can be used, and the total amount of wire is less, reducing the resistance.
In toroid, all the magnetic flux is contained in the core material. This is because the core has no ends from which flux might leak off. The confinement of the flux prevents external magnetic fields from affecting the magnetic field in the toroid from affecting other components in a circuit.
Standard toroidal transformers typically offer a 95% efficiency, while standard laminated transformers typically offer less than a 90% rating.
one of the most important differences between a toroidal transformer and a tradition laminated transformer is the absence of gaps. The leakage flux through the gaps contributes to the stray losses in the form of eddy currents (Which is also expelled in the form of heat).
A toridal core doesn't have an air gap. The core is tightly wound. The result is a stable predictable toroidal core, free from discontinuities and holes.
Audible vibration or hum in transformers is caused by vibration of the windings and core layers from the forces between the coil turns and core laminations. The toroidal transformer's construction helps quiet this noise.
in audio, or signal transmitting applications, unwarranted noise will affect sound quality, so a transformer with low audible vibration is ideal. For this reason, many sound system engineers prefer to use toroidal transformer instead of a traditional laminated transformer.
A toroid has _____ inductance, for a given number of turns, than a solenoid with a core of same material and similar size.
View Solution
Knowledge Check
PQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

External force required to maintain constant velocity of the loop for x=−95a will beAB2a2v2 to the rightBB2a2v2R to the rightCB2a2v2R to the leftDzeroPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=a/4
(i) magnetic flux through the loop,
(ii) induced current in the loop and
(iii) external force required to maintain constant velocity of the loop, will beA(i) Ba2 (ii) Bav2R (iii) B2a2v24R2B(i) Ba2 (ii) zero (iii) zeroC(i) Ba2 (ii) Bav2R (iii) zeroD(i) zero (ii) zero (iii) zeroPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=−9a/5, magnitude of induced current and its direction as seen from above will be:ABav, clockwiseBBavR, clockwiseCzeroDBavR, anticlockwise
III. Read the following text and answer the following questions on the basis of the same:
TOROID
A toroid is a coil of insulated or enamelled wire wound on a donut-shaped form made of powdered iron. A toroid is used as an inductor in electronic circuits, especially at low frequencies where comparatively large inductances are necessary.
A toroid has more inductance, for a given number of turns, than a solenoid with a core of the same material and similar size. This makes it possible to construct high-inductance coils of reasonable physical size and mass. Toroidal coils of a given inductance can carry more current than solenoidal coils of similar size, because large-diameter wires can be used, and the total amount of wire is less, reducing the resistance.
In toroid, all the magnetic flux is contained in the core material. This is because the core has no ends from which flux might leak off. The confinement of the flux prevents external magnetic fields from affecting the magnetic field in the toroid from affecting other components in a circuit.
Standard toroidal transformers typically offer a 95% efficiency, while standard laminated transformers typically offer less than a 90% rating.
one of the most important differences between a toroidal transformer and a tradition laminated transformer is the absence of gaps. The leakage flux through the gaps contributes to the stray losses in the form of eddy currents (Which is also expelled in the form of heat).
A toridal core doesn't have an air gap. The core is tightly wound. The result is a stable predictable toroidal core, free from discontinuities and holes.
Audible vibration or hum in transformers is caused by vibration of the windings and core layers from the forces between the coil turns and core laminations. The toroidal transformer's construction helps quiet this noise.
in audio, or signal transmitting applications, unwarranted noise will affect sound quality, so a transformer with low audible vibration is ideal. For this reason, many sound system engineers prefer to use toroidal transformer instead of a traditional laminated transformer.
Why inductance of solenoid is more than the inductance of a solenoid having same number of turns, core of same material and similar size?
View SolutionIII. Read the following text and answer the following questions on the basis of the same:
TOROID
A toroid is a coil of insulated or enamelled wire wound on a donut-shaped form made of powdered iron. A toroid is used as an inductor in electronic circuits, especially at low frequencies where comparatively large inductances are necessary.
A toroid has more inductance, for a given number of turns, than a solenoid with a core of the same material and similar size. This makes it possible to construct high-inductance coils of reasonable physical size and mass. Toroidal coils of a given inductance can carry more current than solenoidal coils of similar size, because large-diameter wires can be used, and the total amount of wire is less, reducing the resistance.
In toroid, all the magnetic flux is contained in the core material. This is because the core has no ends from which flux might leak off. The confinement of the flux prevents external magnetic fields from affecting the magnetic field in the toroid from affecting other components in a circuit.
Standard toroidal transformers typically offer a 95% efficiency, while standard laminated transformers typically offer less than a 90% rating.
one of the most important differences between a toroidal transformer and a tradition laminated transformer is the absence of gaps. The leakage flux through the gaps contributes to the stray losses in the form of eddy currents (Which is also expelled in the form of heat).
A toridal core doesn't have an air gap. The core is tightly wound. The result is a stable predictable toroidal core, free from discontinuities and holes.
Audible vibration or hum in transformers is caused by vibration of the windings and core layers from the forces between the coil turns and core laminations. The toroidal transformer's construction helps quiet this noise.
in audio, or signal transmitting applications, unwarranted noise will affect sound quality, so a transformer with low audible vibration is ideal. For this reason, many sound system engineers prefer to use toroidal transformer instead of a traditional laminated transformer.
Efficiency of toroidal transformer is around ______% which is ____ than laminated core transformer.
View SolutionIII. Read the following text and answer the following questions on the basis of the same:
TOROID
A toroid is a coil of insulated or enamelled wire wound on a donut-shaped form made of powdered iron. A toroid is used as an inductor in electronic circuits, especially at low frequencies where comparatively large inductances are necessary.
A toroid has more inductance, for a given number of turns, than a solenoid with a core of the same material and similar size. This makes it possible to construct high-inductance coils of reasonable physical size and mass. Toroidal coils of a given inductance can carry more current than solenoidal coils of similar size, because large-diameter wires can be used, and the total amount of wire is less, reducing the resistance.
In toroid, all the magnetic flux is contained in the core material. This is because the core has no ends from which flux might leak off. The confinement of the flux prevents external magnetic fields from affecting the magnetic field in the toroid from affecting other components in a circuit.
Standard toroidal transformers typically offer a 95% efficiency, while standard laminated transformers typically offer less than a 90% rating.
one of the most important differences between a toroidal transformer and a tradition laminated transformer is the absence of gaps. The leakage flux through the gaps contributes to the stray losses in the form of eddy currents (Which is also expelled in the form of heat).
A toridal core doesn't have an air gap. The core is tightly wound. The result is a stable predictable toroidal core, free from discontinuities and holes.
Audible vibration or hum in transformers is caused by vibration of the windings and core layers from the forces between the coil turns and core laminations. The toroidal transformer's construction helps quiet this noise.
in audio, or signal transmitting applications, unwarranted noise will affect sound quality, so a transformer with low audible vibration is ideal. For this reason, many sound system engineers prefer to use toroidal transformer instead of a traditional laminated transformer.
Why sound system engineers prefer to use toroidal transformer?
View SolutionIII. Read the following text and answer the following questions on the basis of the same:
TOROID
A toroid is a coil of insulated or enamelled wire wound on a donut-shaped form made of powdered iron. A toroid is used as an inductor in electronic circuits, especially at low frequencies where comparatively large inductances are necessary.
A toroid has more inductance, for a given number of turns, than a solenoid with a core of the same material and similar size. This makes it possible to construct high-inductance coils of reasonable physical size and mass. Toroidal coils of a given inductance can carry more current than solenoidal coils of similar size, because large-diameter wires can be used, and the total amount of wire is less, reducing the resistance.
In toroid, all the magnetic flux is contained in the core material. This is because the core has no ends from which flux might leak off. The confinement of the flux prevents external magnetic fields from affecting the magnetic field in the toroid from affecting other components in a circuit.
Standard toroidal transformers typically offer a 95% efficiency, while standard laminated transformers typically offer less than a 90% rating.
one of the most important differences between a toroidal transformer and a tradition laminated transformer is the absence of gaps. The leakage flux through the gaps contributes to the stray losses in the form of eddy currents (Which is also expelled in the form of heat).
A toridal core doesn't have an air gap. The core is tightly wound. The result is a stable predictable toroidal core, free from discontinuities and holes.
Audible vibration or hum in transformers is caused by vibration of the windings and core layers from the forces between the coil turns and core laminations. The toroidal transformer's construction helps quiet this noise.
in audio, or signal transmitting applications, unwarranted noise will affect sound quality, so a transformer with low audible vibration is ideal. For this reason, many sound system engineers prefer to use toroidal transformer instead of a traditional laminated transformer.
Toroid is a
View SolutionThe figure shows a uniform, 3.0 T magnetic field that is normal to the plane of a conducting, circular loop with a resistance of 1.5 Ω and a radius of 0.024 m. The magnetic field is directed out of the paper as shown . Note: The area of the non-circular portion of the wire is considered negligible compared to that of the circular loop.
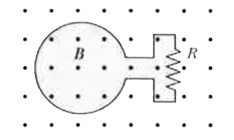
If the magnetic field is held constant at 3.0 T and the loop is pulled out of the region that contains the field in 0.2 s, at what rate is energy dissipated in R?
View Solution
