A diametrical tunnel is dug across the earth. A ball dropped into the tunnel from one side. The velocity of the ball when it reaches the centre of the earth is [Given: gravitational potential at the centre of earth =−3/(2GM/R)]
√R
√gR
√2.5gR
√7.1gR
The correct Answer is:B
Gravitational potential at a point on the surface of earth is −GMR
If the earth is assumed to be a solid sphere, then the gravitational potential at the centre of the earth is (32GM/R).
Decrease in gravitational potential is
R2×GMR2=Rg2
Loss is potential energy is
R2×GMR2×m
Now gain in kinetic energy = loss is potnetial energy. Therefore.
12mv2=12mgR or v=√gR
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Assume that there is a tunnel in the shape of a circular arc through the earth. Wall of the tunnel is smooth. A ball of mass m is projected into the tunnel at A with speed v. The all comes out of the tunnel at B and escapes out of the gravity of the earth. Mass and radius of the earth are M and R respectively and radius of the circle shaped tunnel is also . Find minimum possible value of v (call it v0) If the ball is projected into the tunnel with speed v0, calculate the normal force applied by the tunnel wall on the ball when it is closest to the centre of the earth. It is given that the closest distance between the ball and the centre of the earth is R2

View SolutionA body released at the distance r(r>R) from the centre of the earth. What is the velocity of the body when it strikes the surface of the earth?
View Solution
Knowledge Check
If a tunnel is dug along the diameter of the earth and a ball is dropped into the tunnel, it will have
Alinear motionBcircular motionCoscillatory motionDtranslatory motionA hole is drilled along the diameter of the earth and pen is dropped into it. The time taken by it is reach other end of the earth is
A162.2 minB84.6 minC21.2 minD42.3 minThe diagram showing the variation of gravitational potential of earth with distance from the centre of earth is
A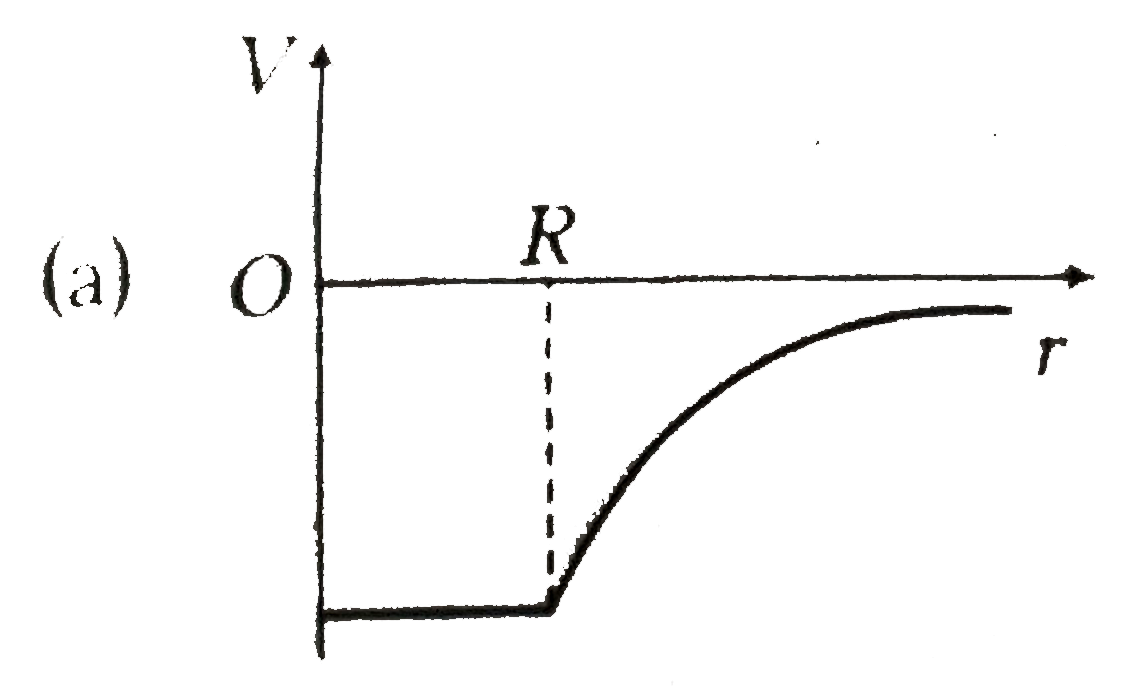 B
B C
C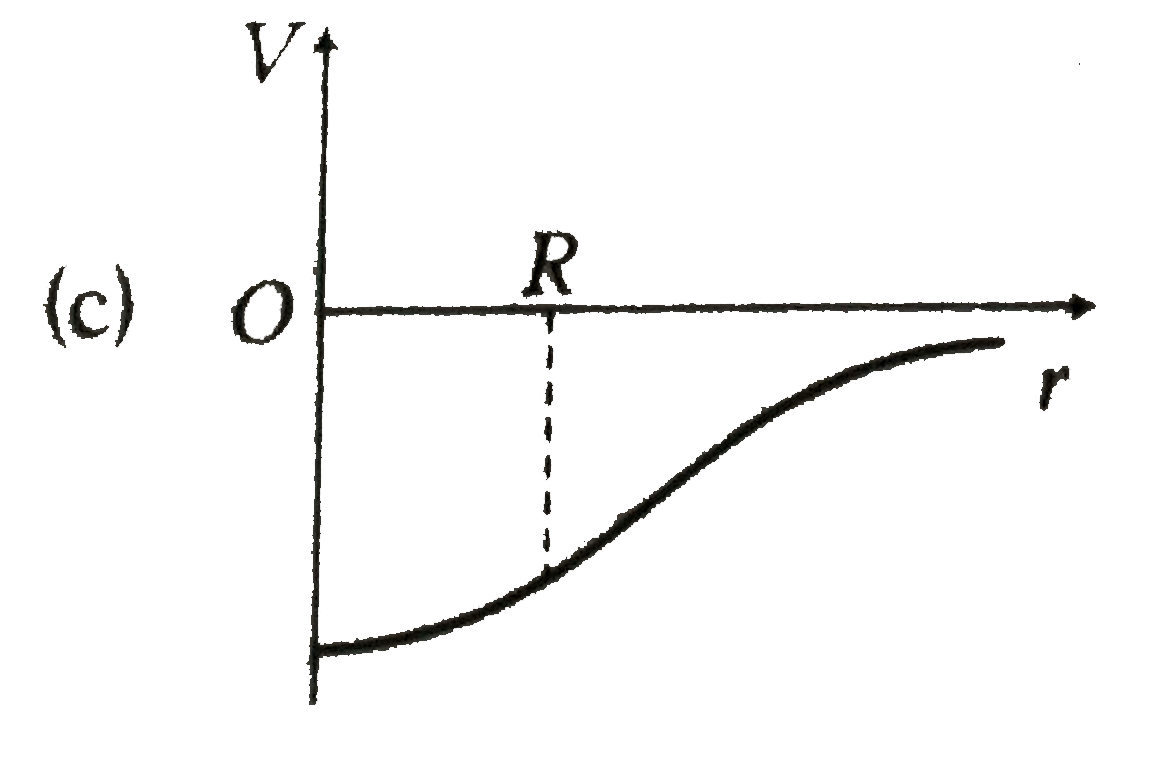 D
D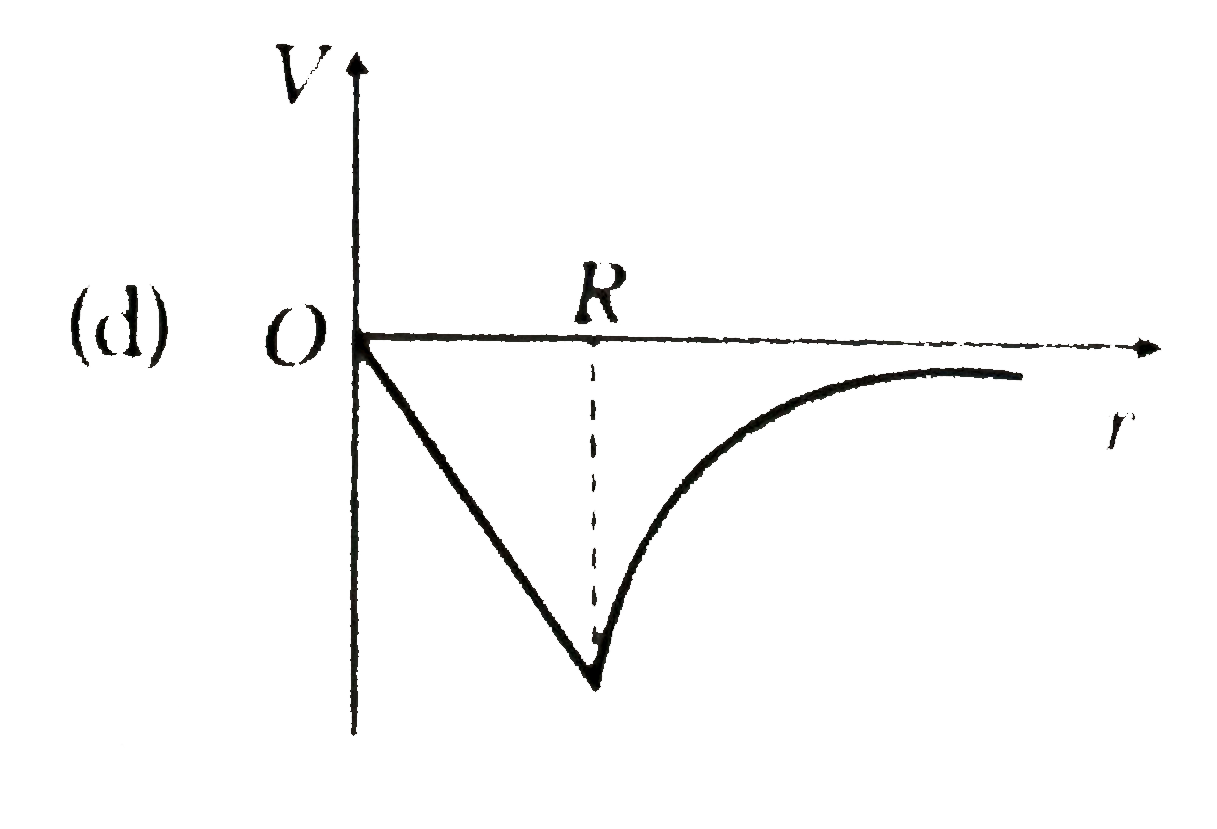
The diagram showing the variation of gravitational potential of earth with distance from the centre of earth is
View SolutionIf V is the gravitational potential on the surface of the earth, then what is its value at the centre of the earth ?
View SolutionA tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance R2 from centre of earth is (where R = radius of Earth and M = mass of Earth)
View SolutionIf potential at the surface of earth is assigned zero value , then potential at centre of earth will be (Mass = M Radius = R)
View SolutionIf a tunnel is dug along the diameter of earth and a piece of stone is dropped into it, then the stone will
View Solution
