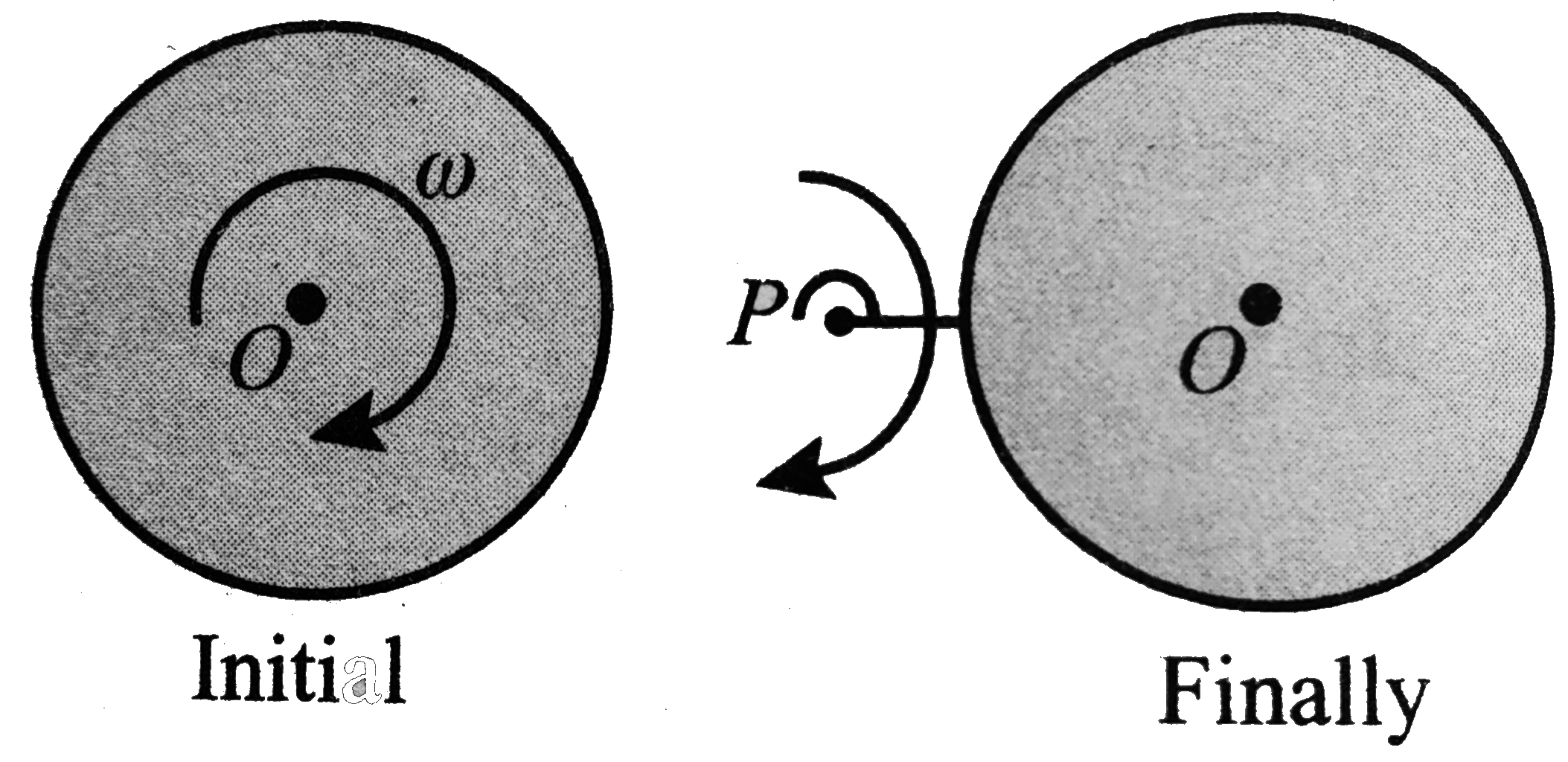
A disc is freely rotating with an angular speed on a smooth horizontal plane. If it is hooked at a rigid pace and rotates without bouncing about a point on its circumference. Its angular speed after the impact will be equal to.
none of the above
The correct Answer is:B
During the impact the impact forces pass through point . Therefore, the torque produced by it about is equal to zero. Cosequently the angular momentum of the disc about , just before and after the impact, remains the same
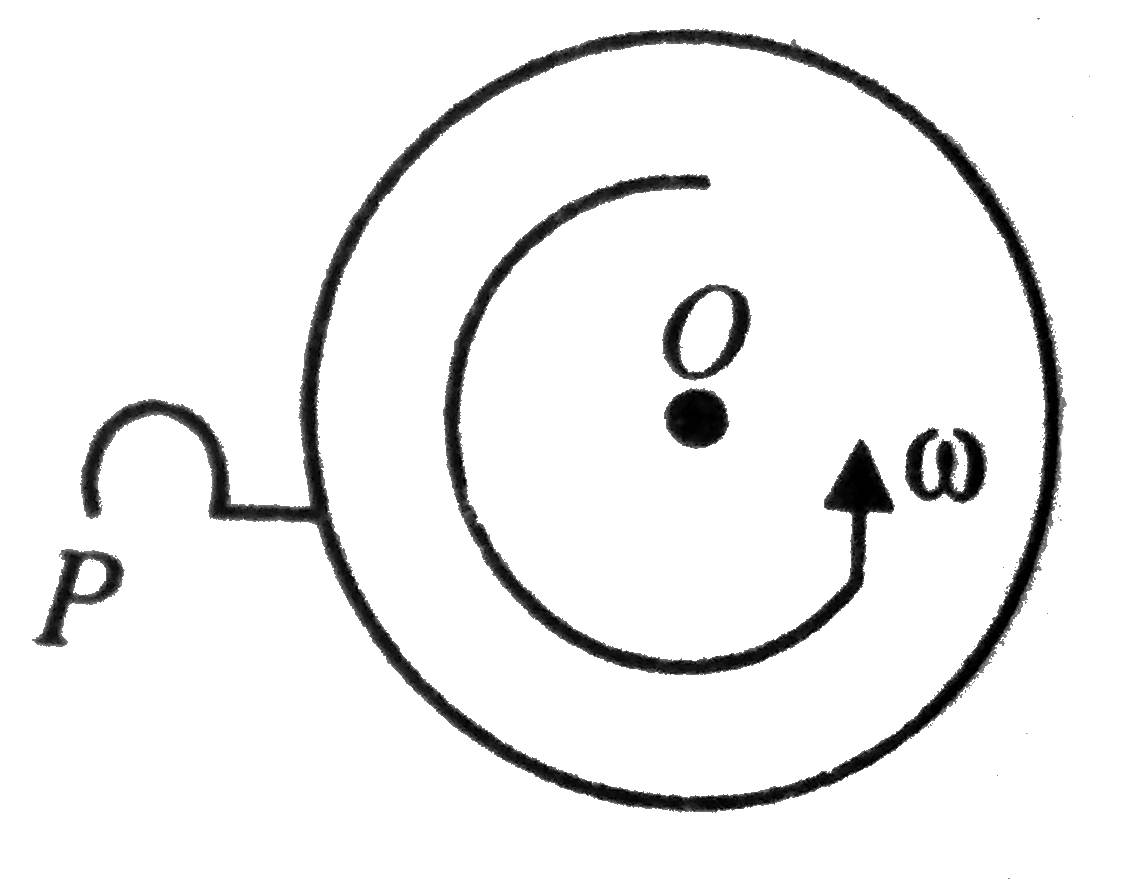
where angular momentum of the disc about just before the impact
Just before the impact the disc rotates about . But just after the impact the disc rotates about .
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
 View Solution
View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
AKinetic energyBPotential energyCLinear momentumDAngular momentum - Question 2 - Select One
A disc is rotating with angular speed CD. If a child sits on it, what is conserved
Alinear momentumBangular momentumCkinetic energyDpotential energy - Question 3 - Select One
A disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
A(1/2)MR2ωBMR2ωC(3/2)MR2ωD2MR2ω
A particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA uniform disc of radius 'a' and mass 'm' is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle of mass 'm' is then suddenly attached to the rim of the disc and rotates with it. The new angular speed is
View SolutionA disc rotates with angular velocity ω and kinetic energy E. Then its angular momentum
View SolutionTwo identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
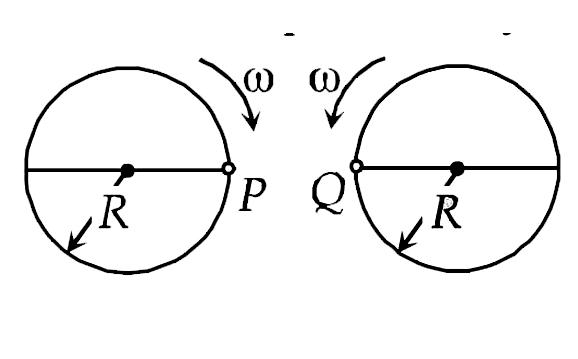 View Solution
View Solution

