A disc is performing pure rolling on a smooth stationary surface with constant angular velocity as shown in Fig,. At any instant, for the lower most point of the disc,
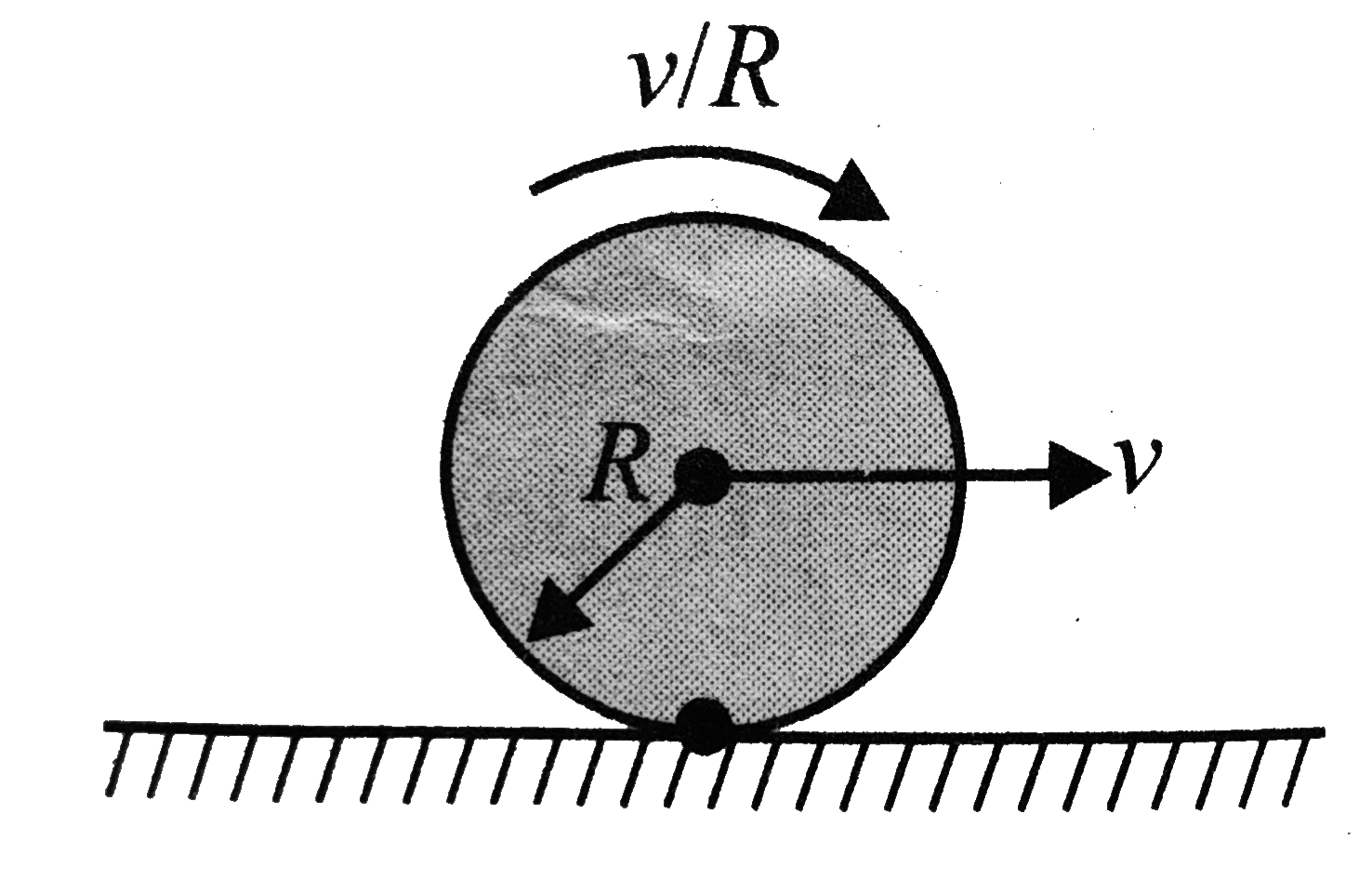
velocity is v, acceleration is zero
velocity is zero, acceleration is zero
velocity is v, acceleration is v2/R
velocity is 0, acceleration is v2/R
The correct Answer is:D
As the disc is in combined rotation and translation each point has a tangential velocity and a linear velocity in the forward direction. From the figure. 
Vnet (for the lowest point) =v
Rω=v−v0 and acceleration v2R+0=v2R
(since the linear speed is constant)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A disc is undergoing rolling on a horizontal surface. Which of the statement about angular momentum of the disc is incorrect ?
View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.
View Solution
Knowledge Check
- Question 1 - Select One
A sphere is performing pure rolling on a rough horizontal surface with constant angular velocity. Frictional force acting on the sphere is zero.
Velocity of contact point is zero.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True. - Question 2 - Select One or More
A ring performs pure rolling on a horizontal surface and its state at some instant of time is shown in figure.
AK.E. stored in the portion AB is same as K.E. stored in the portion CDBK.E. stored in the portion AB is same as KE. stored in the portion BCCK.E. stored in the portion ABC is same as K.E. stored in the portion CDADK.E. stored in the portion ABC is less than K.E. stored in the portion CDA - Question 3 - Select One
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
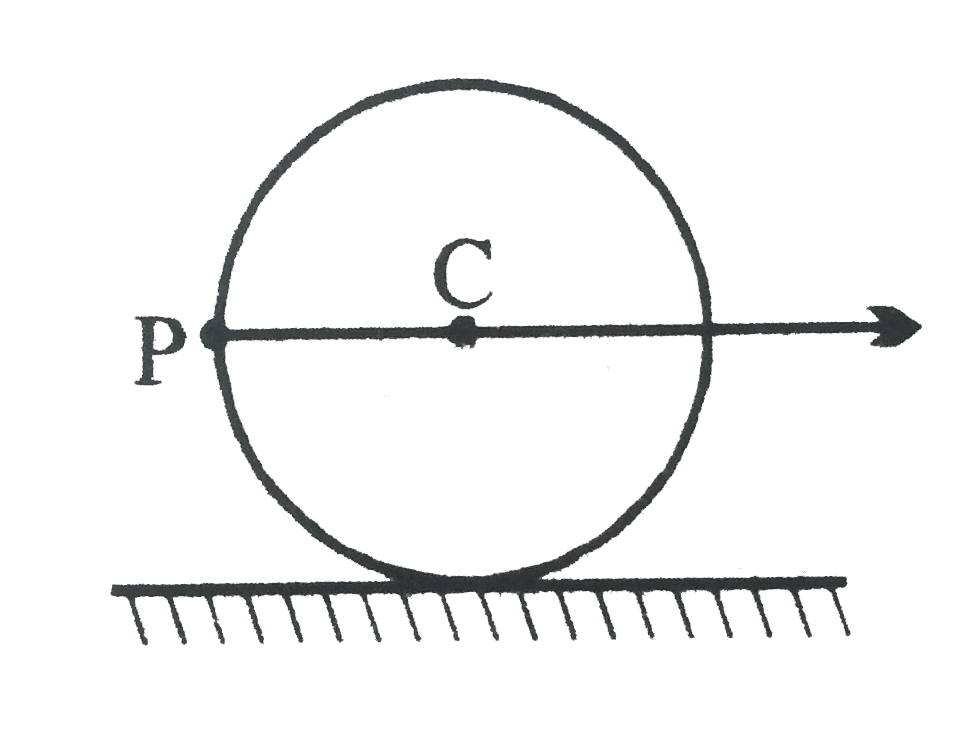.AzeroB45∘C135∘Dtan−1(1/2)
An object of mass M and radius R is performing pure rolling motion on a smooth horizontal surface under the action of a constant force F as shown in Fig. The object may be
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isView SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
View SolutionA ball of radius r is rolling (pure rolling) on a convex stationary circular surface of radius R with angular velocity ω and angular acceleration α. The magnitude of vertical acceleration of top point of the ball is
View SolutionA disc of mass 4.8 kg and radius 1 m is rolling on a horizontal surface without sliding with angular velocity of 600 rotations/min. What is the total kinetic energy of the disc ?
View Solution