
A disc of mass M and radius R is rolling purely with centre's velcity v0 on a flat horizontal floor when it hits a step in the floor of height R/4 The corner of the step is sufficiently rough to prevent any slippoing of the disc against itself. What is the velocity of the centre of the disc just after impact?
4v0/5
4v0/7
5v0/6
none of these

Angular momentum will remain conserved at the point of impact P, and just after impact it start rotating about point P.
∴Mv0(R−R4)+12MR2(v0R)=32MR2.ω
∴ω=5v06R
∴vCOM=ωR=5v06
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts with a purely sliding motion at t= 0. After t0 seconds it acquires a purely rolling motion.
(a) Calculate the velocity of the centre of mass of the disc at t0
(b) Assuming the coefficient of friction to be μ, calculate to. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t muchlonger than t0.
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at t0.
Assuming that the coefficent of friction to be μ, calculate t0.

View Solution
Knowledge Check
A disc of radius 0.2m is rolling with slipping on a flat horizontal surface, as shown in Fig. The instantaneous centre of rotation is (the lowest contact point is O and centre of disc is C)
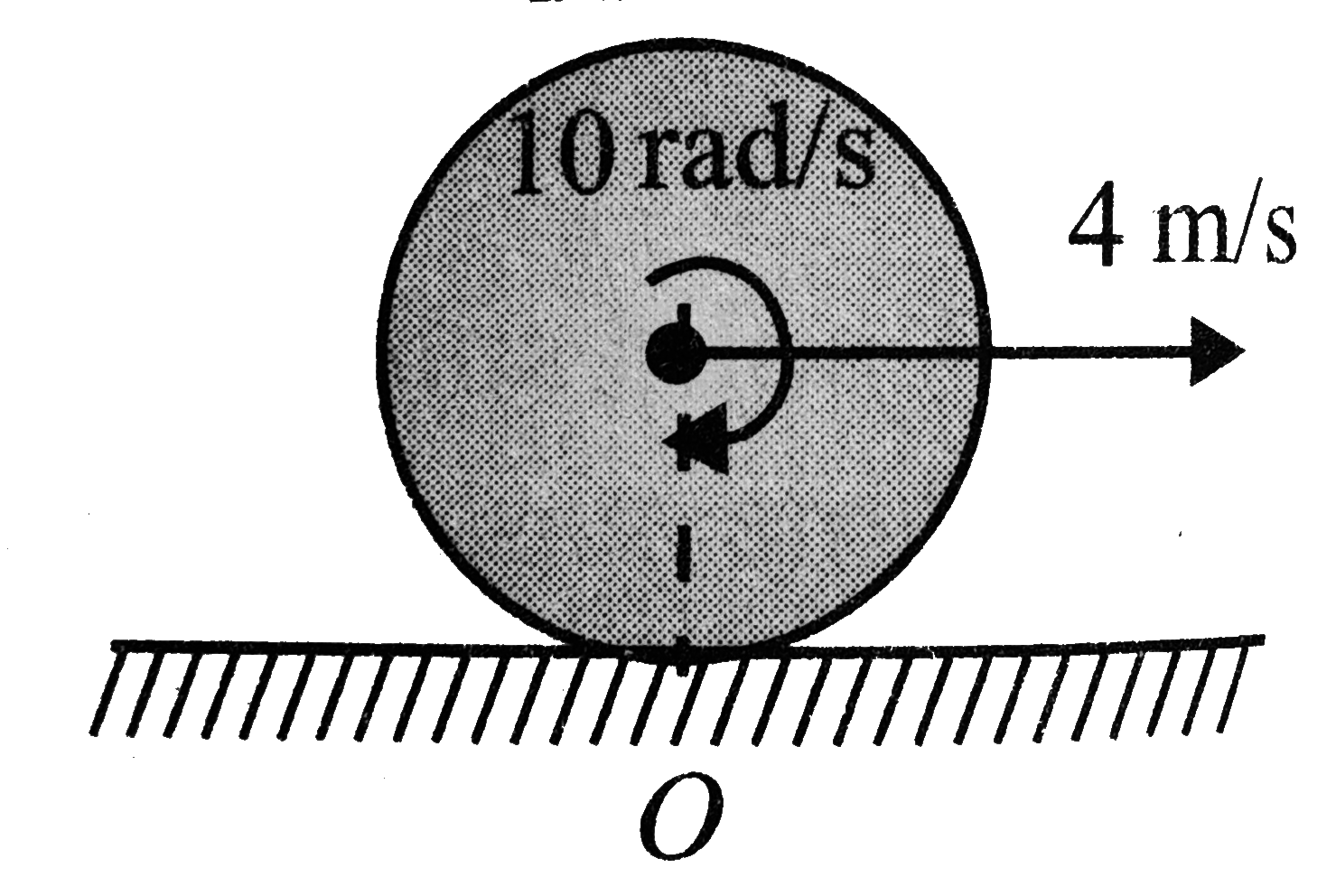 AzeroB0.1m above O on line OCC0.2m below O on line OCD0.2m above O on line OC
AzeroB0.1m above O on line OCC0.2m below O on line OCD0.2m above O on line OC
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isAzeroB45∘Ctan−1(2)Dtan−1(1/2)A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
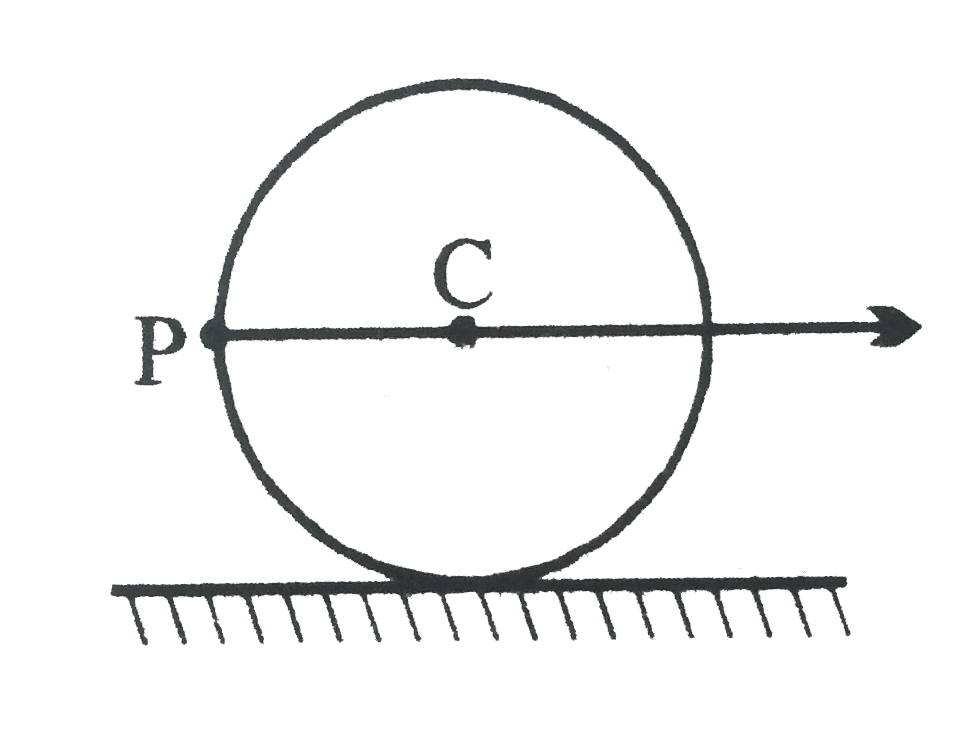 .AzeroB45∘C135∘Dtan−1(1/2)
.AzeroB45∘C135∘Dtan−1(1/2)
A sphere of mass m and radius R is kept on a rough horizontal floor. Constant force Facts at the top point of sphere along tangent. If there is sufficient friction on the floor to support pure rolling then calculate acceleration of sphere.
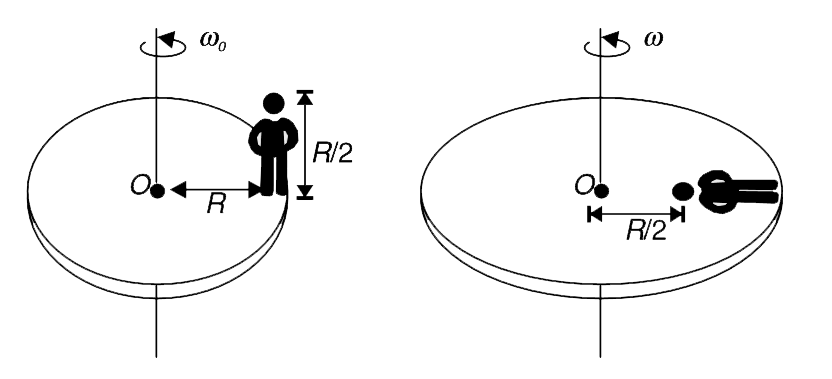
View SolutionA disc of mass M and radius R is rotating with angular velocity ω0 about a vertical axis passing through its centre (O). A man of mass M2 and height R2 is standing on the periphery. The man gradually lies down on the disc such that his head is at a distance R2 from the centre and his feet touching the edge of the disc. For simplicity assume that the man can be modelled as a thin rod of length R2. Calculate the angular speed (ω) of the platform after the man lies down.
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA uniform disc of mass 'm' and radius R is placed on a smooth horizontal floor such that the plane surface of the disc in contact with the floor . A man of mass m/2 stands on the disc at its periphery . The man starts walking along the periphery of the disc. The size of the man is negligible as compared to the size of the disc. Then the center of disc.

View Solution
