A dog sees a flowerpot that sails first up and then down past an open window. The pot is in view for a total of 0.50 s, and the top-to-bottom height of the window is 2.00 m. How high above the window top does the flowerpot go ?
The correct Answer is:2.34 m
To solve the problem of how high above the window top the flowerpot goes, we can follow these steps:
Step 1: Understand the Motion
The flowerpot moves upward and then downward, passing by the window. The total time it is in view is 0.50 seconds, and the height of the window is 2.00 meters.
Step 2: Determine the Initial Conditions
When the flowerpot passes the top of the window, we can assume its initial velocity (u) is 0 m/s at the highest point of its trajectory. The flowerpot then falls down past the window.
Step 3: Calculate the Final Velocity at the Bottom of the Window
Using the kinematic equation:
v2=u2+2gh
Where:
- v = final velocity
- u = initial velocity (0 m/s at the top)
- g = acceleration due to gravity (approximately 9.8 m/s²)
- h = height of the window (2 m)
Substituting the values:
v2=0+2×9.8×2
v2=39.2
v=√39.2≈6.26m/s
Step 4: Calculate the Time to Fall Through the Window
The time to fall through the window can be calculated using the formula:
t=hv
Where h is the height of the window (2 m) and v is the velocity at the bottom of the window (6.26 m/s).
t=26.26≈0.319s
Step 5: Determine the Time to Reach the Highest Point
Since the total time the flowerpot is in view is 0.50 seconds, we can find the time taken to reach the highest point:
tup=0.50−tfall
tup=0.50−0.319≈0.181s
Step 6: Calculate the Maximum Height Above the Window
Using the time to reach the highest point, we can calculate the height above the window using the formula:
hmax=ut+12gt2
Where:
- u=6.26m/s (initial velocity at the bottom of the window)
- t=0.181s
Substituting the values:
hmax=6.26×0.181+12×9.8×(0.181)2
hmax=1.134+0.161≈1.295m
Final Step: Total Height Above the Window
Since the height of the window is 2 m, the total height above the window is:
htotal=hmax+hwindow
htotal=1.295+2≈3.295m
Conclusion
The flowerpot goes approximately 1.295 meters above the top of the window.
---
The flowerpot moves upward and then downward, passing by the window. The total time it is in view is 0.50 seconds, and the height of the window is 2.00 meters.
When the flowerpot passes the top of the window, we can assume its initial velocity (u) is 0 m/s at the highest point of its trajectory. The flowerpot then falls down past the window.
Using the kinematic equation:
v2=u2+2gh
Where:
- v = final velocity
- u = initial velocity (0 m/s at the top)
- g = acceleration due to gravity (approximately 9.8 m/s²)
- h = height of the window (2 m)
v2=0+2×9.8×2
v2=39.2
v=√39.2≈6.26m/s
The time to fall through the window can be calculated using the formula:
t=hv
Where h is the height of the window (2 m) and v is the velocity at the bottom of the window (6.26 m/s).
t=26.26≈0.319s
Since the total time the flowerpot is in view is 0.50 seconds, we can find the time taken to reach the highest point:
tup=0.50−tfall
tup=0.50−0.319≈0.181s
Using the time to reach the highest point, we can calculate the height above the window using the formula:
hmax=ut+12gt2
Where:
- u=6.26m/s (initial velocity at the bottom of the window)
- t=0.181s
hmax=6.26×0.181+12×9.8×(0.181)2
hmax=1.134+0.161≈1.295m
Since the height of the window is 2 m, the total height above the window is:
htotal=hmax+hwindow
htotal=1.295+2≈3.295m
The flowerpot goes approximately 1.295 meters above the top of the window.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Single Correct Choice Type)54videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( More than One Correct Choice Type )6videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - Checkpoints5videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
A dog sees a flowerpot sail upand then back down past a window 5 ft high. If the total time the pot is in sight is 1.0 sec, find the height above the window that the pot rises. Take g=32ft/s2
View SolutionA stone drops from the edge of the roof. It passes a window 2 m high in 0⋅1s. How far is the roof above the top of the window?
View Solution
Knowledge Check
- Question 1 - Select One
A ball dropped from the top of a building takes 0.5 sec to clear the window of 4.9 m height. What is the height of building above the window?
A2.75 mB5.0 mC5.5 mD4.9 m - Question 2 - Select One
In a circus, a performer throws an apple towards a hoop held at 45 m height by another performer standing on a high platform (see figure below). The thrower aim s for the hoop and throws the apple with a speed of 24 m/s.
At the exact moment that the thrower released the apple, the other performer drops the hoop.
The hoop falls straight down. At what height above the ground does the apple go through the hoop ?
 A21 mB22 mC23 mD24 m
A21 mB22 mC23 mD24 m
A ball is dropped from the top of a building. The ball takes 0.50s to fall past the 3m length of a window, which is some distance below the top of the building.
(a) How fast was the ball going as it passed the top of the window?
(b) How far is the top of the window from the point at which the ball was dropped?
Assume acceleration g in free fall due to gravity to be 10m/s2 downwards.View SolutionA steel ball is dropped from th roof of a building. A man standing in front of a 1−m high window in the building notes tha the ball takes 0.1s to the fall from the top to the boottom of the window. The ball continues to fall and strikes the ground. On striking the ground, the ball gers rebounded with the same speed with which it hits the ground. If the ball reappears at the bottom of the window 2s after passing the bottom of the window on the way down, dind the height of the building.
View SolutionConsider a water tank as shown in the figre. It's cross-sectional area is 0.4m2. The tank has an opening B near the bottom whose cross-section area is 1cm2. A load of 24kg is applied on the water at the top when the height of the water level is 40 cm above the bottom, the velocity of water combing out the opening B is v ms−1. The value of v, to be nearest integer, is [Take value of g to be 10ms−2]
 View Solution
View SolutionA steel ball is dropped from the roof of a building.An observer standing in front of a window 1.2 m high notes that the ball takes 18 s to fall from the top to the bottom of the window.The ball continues to fall, makes a completely elastic collision with a horizontal sidewalk and reappears at the bottom of the window 2 s after passing it on the way down. How tall is the building ?
View SolutionA train ball is dropped from the roof of a building. An observer standing in front of a window 1.2m high notes that the ball takes 18s to fall from the top to the bottom of the window. The ball continues to fall , makes a completely elastic collision with a horizontal sidewalk and reappears at the bottom of the window 2 s after passing in on the way down. How tall is the building ?
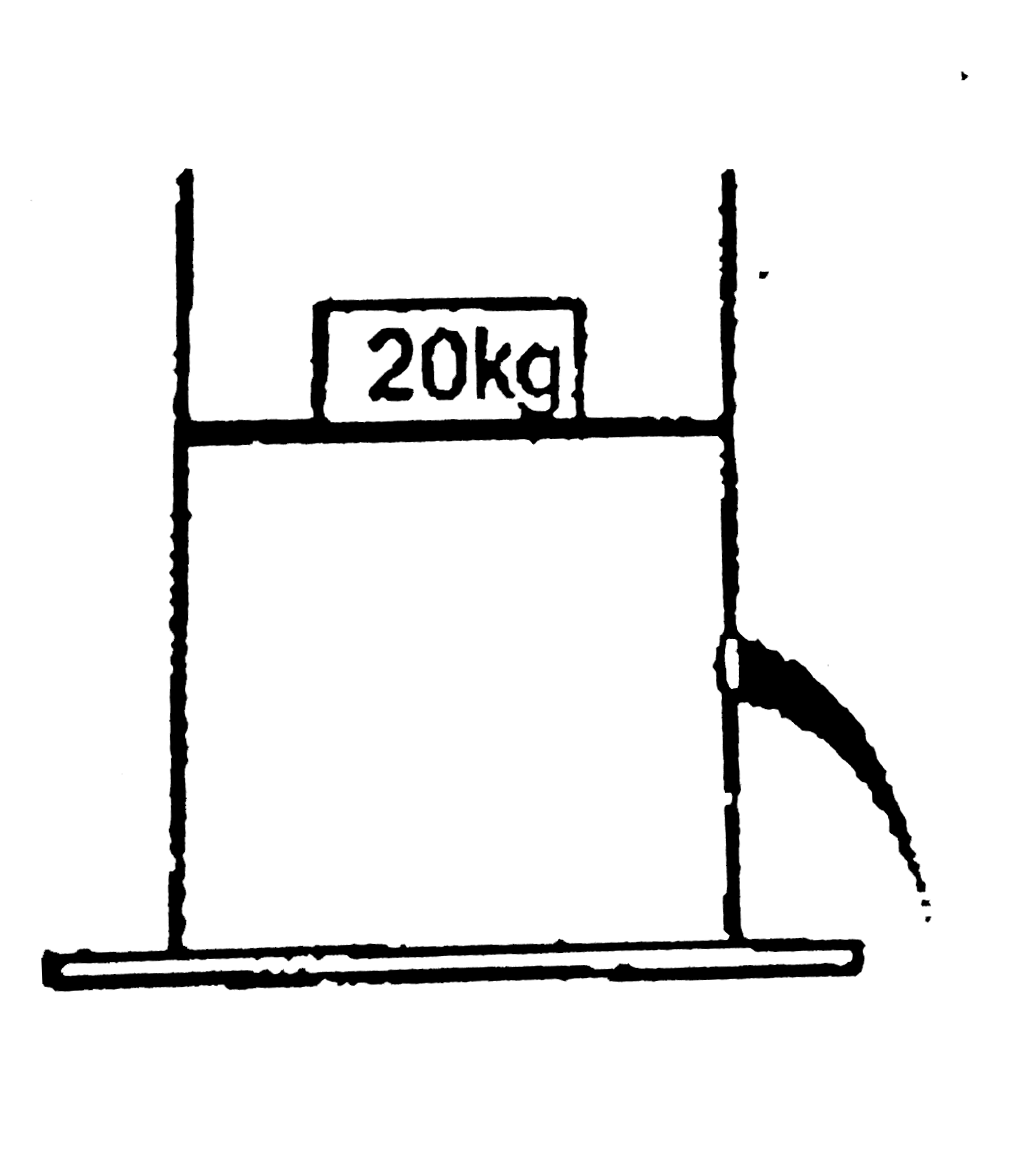
View SolutionA long cylindrical tank of cross-section area 0.5m2 is filled with water. It has an opening at a height 50 cm from the bottom, having area of cross-section 1×10−4m2. A movable piston of cross-section area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20 kg is applied on the top of the water by piston, as shown in the figure. Find the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston). If this speed is (18x) m/s, find the value of x.
 View Solution
View Solution

