A driver accelerates his car first at the rate of 1.8m/s2 and then at the rate of 1.2m/s2. The ratio of the forces exerted by the engines will be respectively equal to
2:3
1:2
2:1
3:2
The correct Answer is:D
To solve the problem of finding the ratio of forces exerted by the engines during two different accelerations, we can follow these steps:
1. Understand the relationship between force and acceleration:
According to Newton's second law of motion, the force exerted by an object is directly proportional to its acceleration. This can be expressed as:
F=m⋅a
where F is the force, m is the mass, and a is the acceleration.
2. Set up the ratio of forces:
Since the mass of the car remains constant during both accelerations, we can express the ratio of the forces exerted by the engines during the two different accelerations as:
F1F2=m⋅a1m⋅a2
Here, a1 is the first acceleration (1.8 m/s²) and a2 is the second acceleration (1.2 m/s²). The mass m cancels out, leading to:
F1F2=a1a2
3. Substitute the values of acceleration:
Now, substitute the given values of acceleration into the equation:
F1F2=1.8m/s21.2m/s2
4. Simplify the ratio:
To simplify the ratio:
F1F2=1.81.2=1812
Now, divide both the numerator and the denominator by 6:
F1F2=32
5. State the final answer:
Therefore, the ratio of the forces exerted by the engines is:
F1:F2=3:2
According to Newton's second law of motion, the force exerted by an object is directly proportional to its acceleration. This can be expressed as:
F=m⋅a
where F is the force, m is the mass, and a is the acceleration.
Since the mass of the car remains constant during both accelerations, we can express the ratio of the forces exerted by the engines during the two different accelerations as:
F1F2=m⋅a1m⋅a2
Here, a1 is the first acceleration (1.8 m/s²) and a2 is the second acceleration (1.2 m/s²). The mass m cancels out, leading to:
F1F2=a1a2
Now, substitute the given values of acceleration into the equation:
F1F2=1.8m/s21.2m/s2
To simplify the ratio:
F1F2=1.81.2=1812
Now, divide both the numerator and the denominator by 6:
F1F2=32
Therefore, the ratio of the forces exerted by the engines is:
F1:F2=3:2
Topper's Solved these Questions
- LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEBOOK - MCGROW HILL PUBLICATIONCHAPTER - LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEEXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
- HEATING AND MAGNETIC EFFECTS OF CURRENT BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEATING AND MAGNETIC EFFECTS OF CURRENT EXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
- MEASUREMENTBOOK - MCGROW HILL PUBLICATIONCHAPTER - MEASUREMENTEXERCISE - ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)
13 Videos
Similar Questions
A car accelerates from rest at the rate of 1m/s2 for 5 seconds and then retards at the same rate till it comes to rest. Draw the x-t, v-t and a-t graphs
View SolutionA car is moving on circular path of radius 100 m such that its speed is increasing at the rate of 5ms2 at t=0 it starts from rest. The radial acceleration of car at the instant it makes one compelete round trip, will be equal to 10πxms2 then find x.
View Solution
Knowledge Check
A flat plate moves normally towards a discharging jet of water at the rate of 3m/s. The jet discharges the water at the rate of 0.1m3/s and at the speed of 18m8/s. The force exerted on the plate due to the jet is
A1800NB2100NC2450ND1560NA car is moving in a circular path of radius 500m with a speed of 30m/s. If the speed is increased at the rate of 2m/s2, the resultant acceleration will be .
A2m/s2B2.5m/s2C2.7m/s2D4m/s2A car accelerates from rest at a constant rate of 2m/s2 and comes to rest. If it remains in motion for 3 seconds, then the maximum speed attained by the car is :
A2 m/sB3 m/sC4 m/sD6 m/s
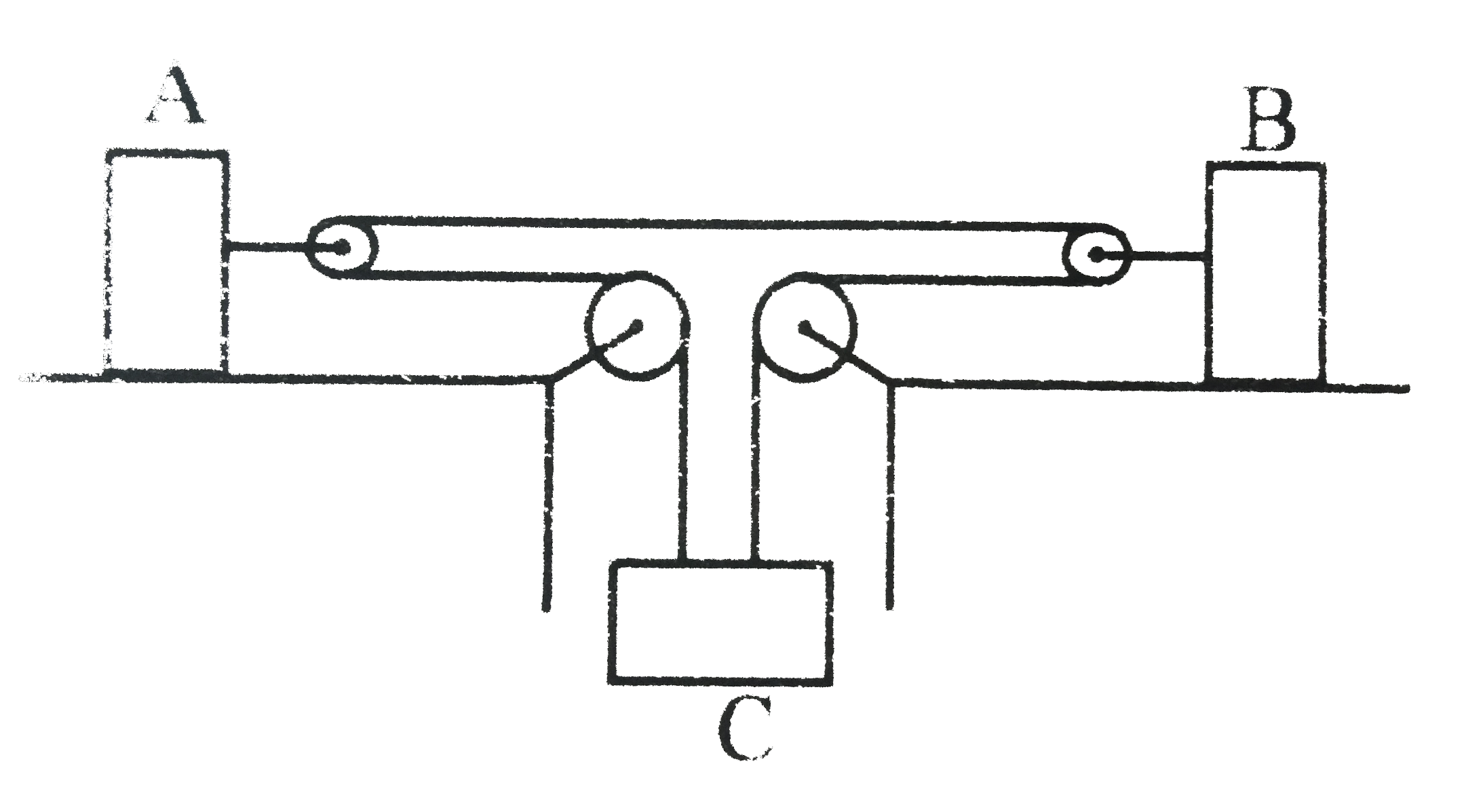
If acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
View SolutionA car acceleration from rest at a constant rate 2m/s2 for some time. Then, it retards at a constant rate of 4m/s2 and comes to rest. If it remains motion for 3 second, then the maximum speed attained by the car is:-
View SolutionA motor car is travelling at 60m/s on a circular road of radius 1200m. It is increasing its speed at the rate of 4m/s2. The acceleration of the car is:
View SolutionA player caught a cricket ball of mass 150g moving at a rate of 20m/s. If the catching process is completed in 0.1s, the force of the blow exerted by the ball on the hand of the player is equal to
View Solution
