A drunkard is walking along a straight road. He takes five steps forward and three steps backward and so on. Each step is 1m long and takes 1s. There is a pit on the road 11m, away from the starting point. The drunkard will fall into the pit after.
21 s
29 s
31 s
37 s
The correct Answer is:B
(b) : Displacement in first eight steps = 5 - 3 = 2 m
Time taken for first eight steps = 8 s
Time taken by the drunkard to cover first 6 m of journey = 82×6= 24 s
If the drunkard takes 5 steps more, he will fall into the pit. So the time taken by the drunkard to cover last five steps = 5 s.
Total time taken = 24 s + 5 s = 29 s
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Average Velocity And Average Speed
8 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Instantaneous Velocity And Speed
16 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, and again takes 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Determine how long the drunkard takes to fall into a pit 13 m away from the start.
View SolutionA drunkard man walking in a narrowlane takes (5) steps forward and 3 steps backward each stepe of (1) m ling, per second and os on. Determine how long the drunkard takes to fall in a pot 15m away from the start.
View Solution
Knowledge Check
A frog walking in a narrow lane takes 5 leaps forward and 3 leaps backward, then again 5 leaps forward and 3 leaps backward, and so on. Each leap is 1m long and requires 1s. Determine how long the frog takes to fall in a pit 13m away from the starting point.
A35 sB36 sC37 sD38 sA man takes a step forward with probability 0.4 and back ward with probability 0.6. The probability that at the end of eleven steps he is one step away from the starting point is:
A11C6(0.1)11B11C6(0.21)5C11C6(0.2)11Dnone of theseA man takes a step forward with probability 0.4 and backward with probability 0.6. The probability that at the end of eleven steps he is just one step away from the starting point, is
A11C5(0.4)6(0.6)5B11C6(0.4)5(0.6)6C11C5(0.4)5(0.6)5DnC5(0.4)5(0.6)5
A drunkard waking in a barrow lane takes 5 steps forward and 3 steps backward, followed again 5 steps forward and 3 steps backward, and so on. Each step is 1mlong and requires 1 s.Determinehowlongthedrunkardtakes→fall∈aπt 13 m away from start.
View SolutionA drunkard waking in a borrow lane takes 6 steps forward and 4 steps backward, following againg 6 steps forward and 4 steps backward and so on Each step is 1m long and requires 1s. Determine how long the drunkard takes to fall in a pit 15m away from the start.
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x−t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1s. Plot the x-t graph of his motion. Determine graphically or otherwise how long the drunkard takes to fall in a pit 9 m away from the start.
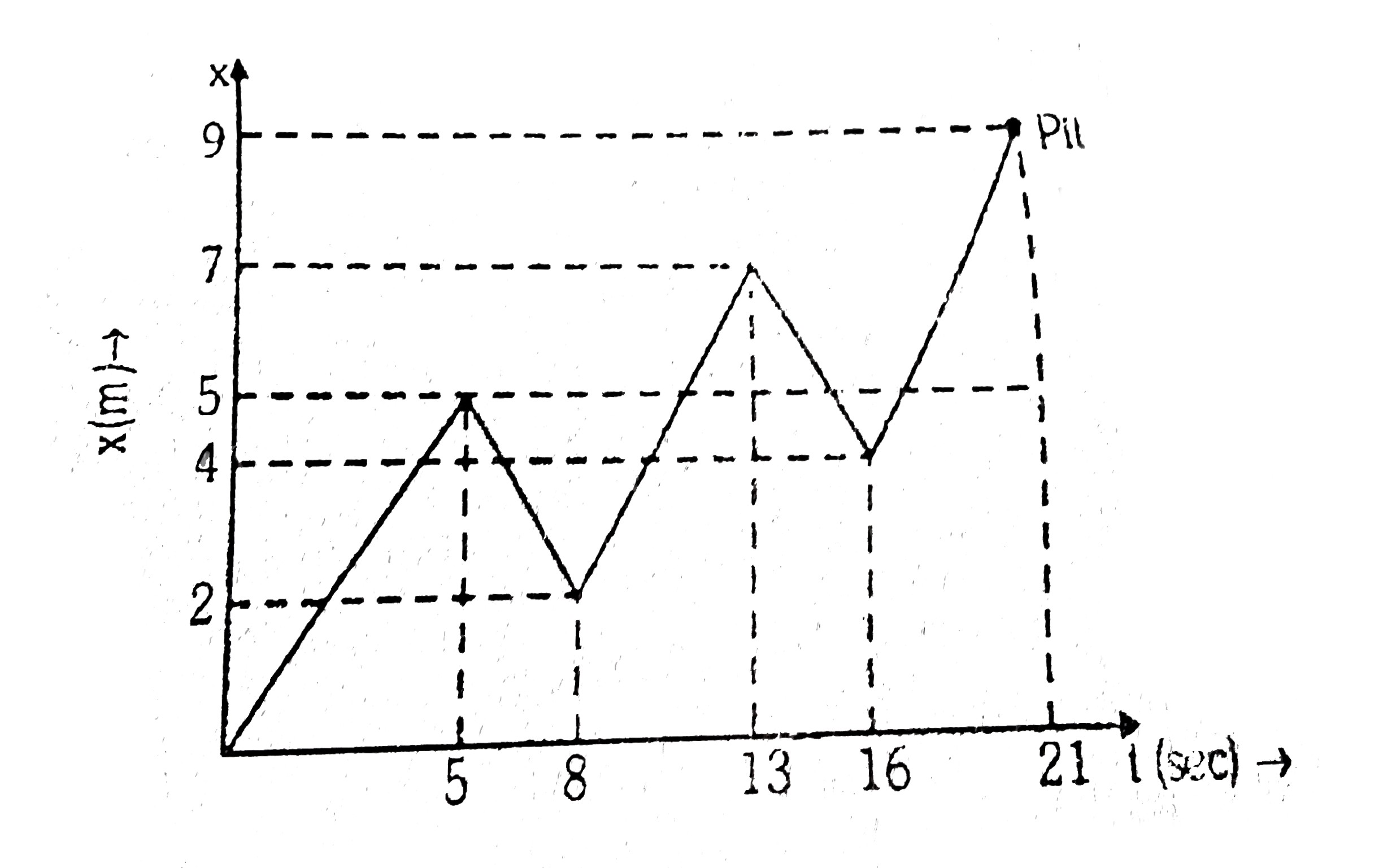
View SolutionA drunkard moves on a straight road such that he takes 7 steps forward and 2 steps backward in each cycle. If the stride length of each step is 1 feet and the drunkard moves with a speed 2 feet/s in forward direction and 4 feet/s in backward direction, then the time after which the drunkard will fall into a pit 11 feet further from his starting point is
View Solution
