A fan makes 2400 rpm. If after it is switched off, it comes to rest in 10 s, then find the number of times it will rotate before it comes to rest after it is switched off.
400
100
200
50
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Convert RPM to Radians per Second
The fan makes 2400 revolutions per minute (rpm). We need to convert this to radians per second (rad/s).
1. Convert rpm to revolutions per second (rps):
Revolutions per second=2400 rpm60 seconds=40 rps
2. Convert revolutions to radians:
Angular velocity(ω1)=40 rps×2π rad/revolution=80π rad/s
Step 2: Use the Angular Deceleration
When the fan is switched off, it comes to rest in 10 seconds. We can find the angular deceleration (α) using the formula:
α=ΔωΔt=ω2−ω1t
Where:
- ω2=0 (final angular velocity)
- ω1=80π rad/s (initial angular velocity)
- t=10 s
Substituting the values:
α=0−80π10=−8π rad/s2
Step 3: Calculate the Total Angle Rotated
We can use the angular motion equation to find the total angle (θ) rotated before coming to rest:
θ=ω1t+12αt2
Substituting the known values:
θ=(80π)(10)+12(−8π)(102)
Calculating each term:
θ=800π+12(−8π)(100)=800π−400π=400π radians
Step 4: Calculate the Number of Rotations
To find the number of rotations, we divide the total angle by 2π (the angle for one complete revolution):
n=θ2π=400π2π=200
Final Answer
The number of times the fan will rotate before it comes to rest is 200 revolutions.
---
The fan makes 2400 revolutions per minute (rpm). We need to convert this to radians per second (rad/s).
Revolutions per second=2400 rpm60 seconds=40 rps
Angular velocity(ω1)=40 rps×2π rad/revolution=80π rad/s
When the fan is switched off, it comes to rest in 10 seconds. We can find the angular deceleration (α) using the formula:
α=ΔωΔt=ω2−ω1t
Where:
- ω2=0 (final angular velocity)
- ω1=80π rad/s (initial angular velocity)
- t=10 s
α=0−80π10=−8π rad/s2
We can use the angular motion equation to find the total angle (θ) rotated before coming to rest:
θ=ω1t+12αt2
Substituting the known values:
θ=(80π)(10)+12(−8π)(102)
Calculating each term:
θ=800π+12(−8π)(100)=800π−400π=400π radians
To find the number of rotations, we divide the total angle by 2π (the angle for one complete revolution):
n=θ2π=400π2π=200
The number of times the fan will rotate before it comes to rest is 200 revolutions.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
Knowledge Check
If S=6t2−t3, then the body comes to rest after time t=
A2 secB3 secC4 secD8 secA table fan, rotating at a speed of 2400 rpm, is switched off and the resulting variation of the rpm with time is shown in the figure. The total number of revolutions of the fan before it comes to rest is
 A420B190C280D380
A420B190C280D380A table fan rotating at a speed of 2400 rpm is switched off and the resulating variation of the revolution/minute time is shown in Fig. The total number of revolutions of the fan before it comes to rest is
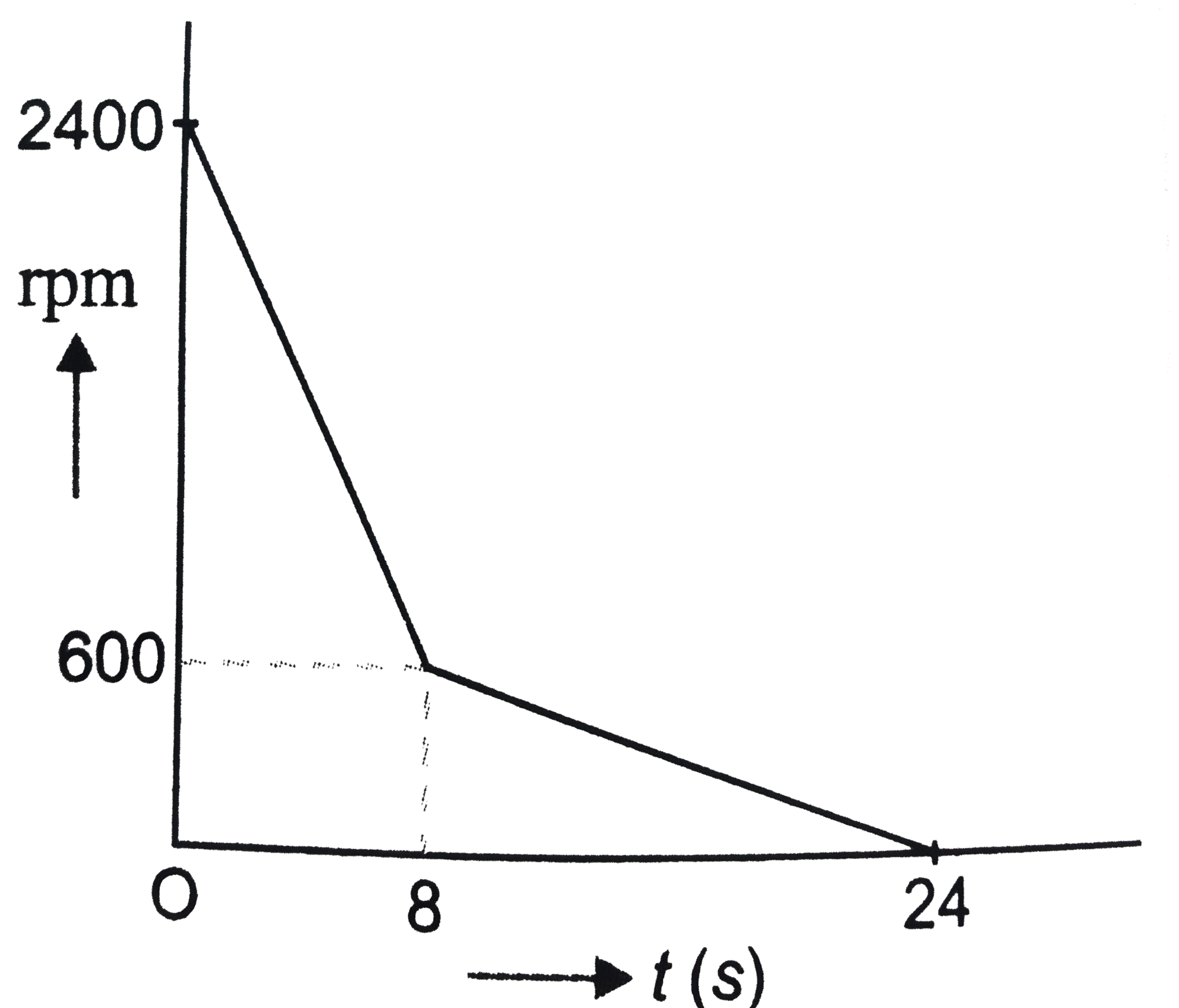 A280B380C420D160
A280B380C420D160
A stirred liquid comes to rest after sometime. Why?
View SolutionA non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.
View SolutionA wheel of a bicycle is rotating about its axis with an angular velocity of 100 rpm. When the brakes are applied, the wheel comes to rest in 10 s. Calculate the number of revolutions made by the wheel before coming to rest. Assume that the deceleration is constant.
View SolutionTwo water drops of radii R1 and R2 are falling with their terminal velocity. If some how gravity is switched off, what is the ratio of their initial accelerations (Just after gravity is switched off)
View SolutionA fan is rotating with a speed of 450 rec/minute. Afer being switched off it comes to rest in 10s. Assuming constant angular deceleration, calculate the number of recvolutions made by it before coming to rest.
View Solution
