A fighter plane flying in the sky describes a vertical circle of radius 150 m when looping with a speed of 420 km/h . The weight of the pilot sitting inside it is 90 kg . With what force the pilot presses his seat when the plane is at the
(i) highest position of circle
(ii) lowest position of circle
To solve the problem of the force exerted by the pilot on his seat at the highest and lowest positions of the vertical circle, we will follow these steps:
Given Data:
- Radius of the circle, r=150m
- Speed of the plane, v=420km/h
- Weight of the pilot, m=90kg
Step 1: Convert Speed from km/h to m/s
To convert the speed from kilometers per hour to meters per second, we use the conversion factor 518.
v=420km/h×518=116.67m/s
Step 2: Calculate the Centripetal Force
The centripetal force required to keep the pilot moving in a circular path is given by the formula:
Fc=mv2r
Step 3: Calculate Forces at the Highest Position
At the highest position, the forces acting on the pilot are:
- Weight of the pilot acting downwards: mg
- Normal force from the seat acting downwards: N1
The net force towards the center (centripetal force) is given by:
mg−N1=Fc
Rearranging gives:
N1=mg−Fc
Substituting the values:
1. Calculate mg:
mg=90kg×10m/s2=900N
2. Calculate Fc:
Fc=90×(116.67)2150
Calculating (116.67)2:
(116.67)2≈13608.89
Now substituting:
Fc=90×13608.89150≈8165.33N
3. Now substituting back to find N1:
N1=900−8165.33≈−7265.33N
Since the normal force cannot be negative, it indicates that the pilot is pressed against the seat with a force of 7265.33N.
Step 4: Calculate Forces at the Lowest Position
At the lowest position, the forces acting on the pilot are:
- Weight of the pilot acting downwards: mg
- Normal force from the seat acting upwards: N2
The net force towards the center is given by:
N2−mg=Fc
Rearranging gives:
N2=mg+Fc
Substituting the values:
1. Using mg=900N from before.
2. We already calculated Fc≈8165.33N.
Now substituting back to find N2:
N2=900+8165.33≈9065.33N
Final Answers:
- (i) At the highest position, the force with which the pilot presses his seat is approximately 7265.33N.
- (ii) At the lowest position, the force with which the pilot presses his seat is approximately 9065.33N.
- Radius of the circle, r=150m
- Speed of the plane, v=420km/h
- Weight of the pilot, m=90kg
To convert the speed from kilometers per hour to meters per second, we use the conversion factor 518.
The centripetal force required to keep the pilot moving in a circular path is given by the formula:
At the highest position, the forces acting on the pilot are:
- Weight of the pilot acting downwards: mg
- Normal force from the seat acting downwards: N1
mg=90kg×10m/s2=900N
Fc=90×(116.67)2150
Calculating (116.67)2:
(116.67)2≈13608.89
Now substituting:
Fc=90×13608.89150≈8165.33N
N1=900−8165.33≈−7265.33N
At the lowest position, the forces acting on the pilot are:
- Weight of the pilot acting downwards: mg
- Normal force from the seat acting upwards: N2
2. We already calculated Fc≈8165.33N.
N2=900+8165.33≈9065.33N
- (i) At the highest position, the force with which the pilot presses his seat is approximately 7265.33N.
- (ii) At the lowest position, the force with which the pilot presses his seat is approximately 9065.33N.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - PRACTICE PROBLEMS27videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions20videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
WAVES
Similar Questions
An aeroplane flying in the sky dives with a speed of 360km/h in a verticale circle of radius 200 m The weight of pilot sitting in it is 75 kg Calulate the force with which the pilot presses his seat when the aeroplane is (i) at the lowest position and (ii) at the highest position Take g=10m/s−2 .
View SolutionAn aeroplane flying in the sky dives with a speed of 360km/h in a verticale circle of radius 200 m The weight of pilot sitting in it is 75 kg Calulate the force with which the pilot presses his seat when the aeroplane is (i) at the lowest position and (ii) at the highest position Take g=10m/s−2 .
View Solution
Knowledge Check
- Question 1 - Select One
A fighter aeroplane flying in the sky dives with a speed of 360km/h in a vertical circle of radius 200 m .Weight of the pilot sitting in it is 75 kg . What will be the value of force with which the pilot presses his seat when the aeroplane is at highest position ? (g=10m/s2)
A3000 NB4500 NC(75×g)ND300 N - Question 2 - Select One
A fighter plane is moving in a vertical circle of radius 'r'. Its minimum velocity at the highest point of the circle will be
A√3grB√2grC√grD√gr/2 - Question 3 - Select One
A pilot of mass 81 kg loops the loop with steady speed of 300km/h. If the radius is 0.5 km then the force with which the pilot is pressed into the seat at the highest point of the loop ,is (g=10m/s2)
A3.15×102NBzeroC8.10×102ND19.35×102N
A particle describes a horizontal circle of radius r on the smooth surface of an inverted cone as shown. The height of plane of circle above vertex is h. The speed of particle should be
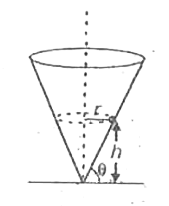 View Solution
View SolutionA fighter jet plane is flying horizontally drops a bomb find the nature of path of bomb as seen by pilot.
View SolutionAn, aeroplane , flying in the sky, suddenly starts revolving in a vertical circle of radius 4 km. At the highest point of the circle , the pilot experiences weightlessness. Its velocity at the highest point will be
View SolutionA fighter plane moves in a vertical circle of radius 2500 m . The mass of the plane is 15000 kg and its speed at the olowest point of its motion is 900 km/ hour . What is the force exerted by air on the plane at the lowest point (g=10m/s2)
View SolutionAn aeroplane flying in the sky with a uniform speed of 200m/s moves in a vertical circle of radius 400 m. The mass of the pilot is 70 kg. The force exerted by the pilot on the seat at the highest point of the circle will be [Take g=10m/s2]
View Solution

