(a) Figure 9.32 shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
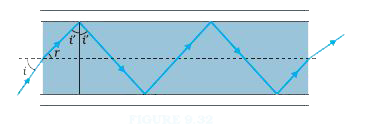
(b) What is the answer if there is no outer covering of the pipe? Solution in Gujrati
⇒ Here, μ1=1.44μ2=1.68
μ2=μ2μ1=1sini.c
But sin ic=μ1μ2=1.441.68=0.8571
∴i.c≈59∘
⇒Ifi.>i.c, then total internal refraction
Hence, if i>59∘ of
refraction angle r<rmax
where rmax=90∘−59∘=31∘
∴ From Snell.s law,
sinimaxsinrmax=μ=1.68
∴sinimax=1.68×sinrmax
=1.68×sin31∘
=1.68×0.5150
=0.8662
∴sinimax≈60∘
∴ Rays enter at 0<i<60∘ with axis of cylinder perform total internal refraction.
⇒ For limited length of pipe, minimum value of incidence angle can be decided by ration of diameter and length of pipe.
(b) If there is no layer outside of pipe, then
sini.c=μ1μ2 where μ1=1,μ2=1.68
=11.68=0.5952
∴ic=36.5∘
∴ F or i=36.5∘,r=36.5∘andi.=90∘−36.5∘
∴i=53.5∘
Thus , i>ic hence 0<i<90∘ , so all the rays perform total internal refraction.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-B (NUMERICALS)(NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK )
12 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-C (NCERT EXEMPLAR SOLUTION) (MULTIPLE CHOICE QUESTIONS (MCQs))
16 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-B (NUMERICALS)(NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
17 Videos
- MOVING CHARGES AND MAGNETISMBOOK - KUMAR PRAKASHANCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - SECTION D (MCQs ASKED IN COMPETITIVE EXAMS)
34 Videos
- SAMPLE QUESTION PAPER BOOK - KUMAR PRAKASHANCHAPTER - SAMPLE QUESTION PAPER EXERCISE - PART-B SECTION-C
5 Videos
Similar Questions
As shown in the figure, a thin rod AB of length 10 cm is placed on the principal axis of a concave mirror such that it.s end B is at a distance of 40 cm from the mirror. If the focal length of the mirror is 20 cm, find the length of the image of the rod

View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is
View SolutionSuppose that the lower half of the concave mirror.s reflecting surface as shown in figure is covered with an opaque (non-reflective) material. What effect will this have on the image of an object placed in front of the mirror ?

View SolutionElectric charge Q having mass M moves on a circular path of radius R with velocity →v, perpendicular to uniform magnetic field B. When a particle completes one revolution, work done by the field is _______
View SolutionTwo charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1 .
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
View Solution(a) Fig. shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68 . The outer covering of the pipe is made of a material of refractive index 1.44 . What is the axis of the pipe for which total reflection inside the pipe take place as shwon. (b) What is the answer if there is no outer covering if the pipe ?
View SolutionIn optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
View Solutionचित्र में अपवर्तनांक 1.68के तन्तु काँच से बनी किसी 'प्रकाश नलिका' (लाइट पाइप) का अनुपर्ष्ठ परिच्छेद दर्शाया गया है| नलिका का बाह्य आवरण 1.44अपवर्तनांक के पदार्थ का बना है| नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण प्रवर्तन होते है, ज्ञात कीजिए |
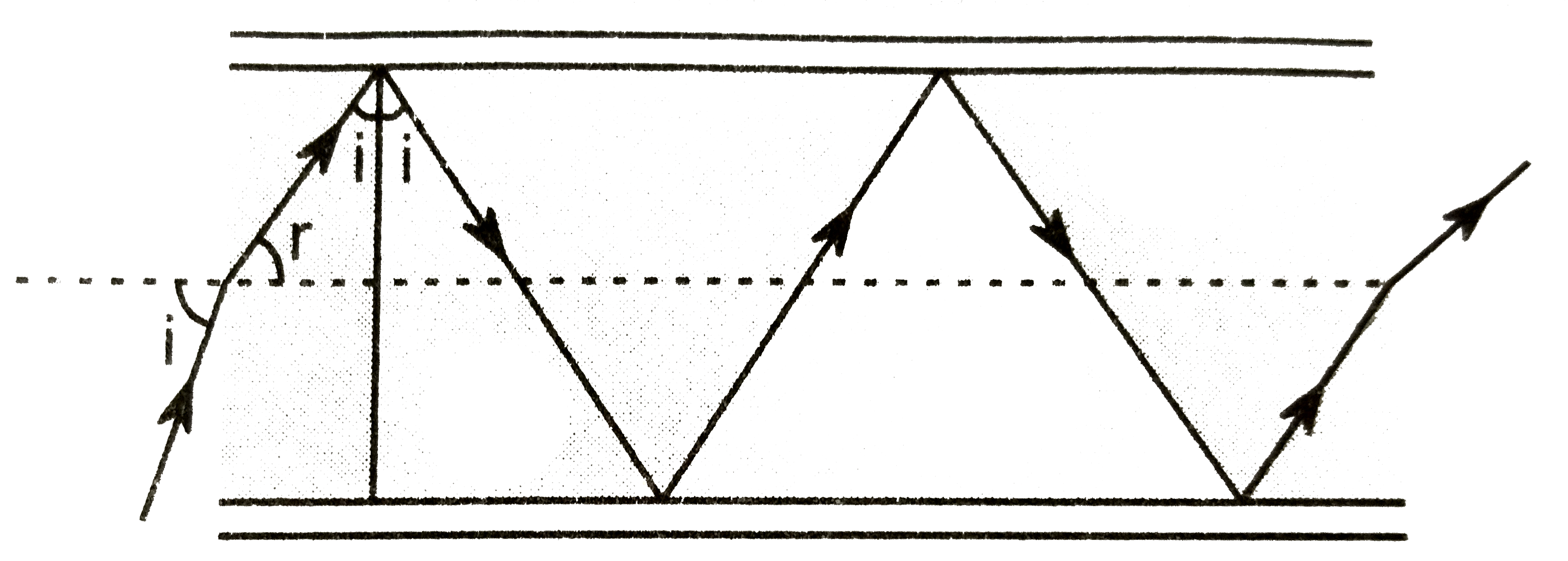
(b) यदि पाइप पर बाह्य आवरण न हो तो क्या उत्तर होगा ?
View Solution(a ) चित्र में अपवर्तनांक 1.68 के काँच तंतु से बनी किसी प्रकाश नालिका का अनुप्रस्थ परिच्छेद दर्शाया गया है। नलिका का बाह्य आवरण ( outer covering ) 1.44 अपवर्तनांक के पदार्थ का बना है। नालिका के अक्ष से आपतित किरणों के कोनों का परिसर ( range ), जिनके लिए चित्र में दर्शाए अनुसार नालिका के भीतर पूर्ण परावर्तन होते है, ज्ञात कीजिए।
(b ) यदि पाइप पर बाह्य आवरण न हो, तो क्या होगा ?

View SolutionA ray of light is incident on a glass. The reflected ray gets totally polarised. The magnitude of incidence angle is (refractive index of glass = μ)
View Solutionचित्र में अपवर्तनांक 1⋅68 के तंतु काँच से बनी किसी 'प्रकाश नलिका' (लाइट पाइप) का अनुप्रस्थ परिच्छेद दर्शाया गया है| नलिका का बाहा आवरण 1⋅44 अपवर्तनांक के पदार्थ का बना है| नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते है ज्ञात कीजिए |
View SolutionIn optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
View Solution(a) Fig. shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the axis of the pipe for which total reflection inside the pipe take place as shwon.
(b) What is the answer if there is no outer covering if the pipe ?
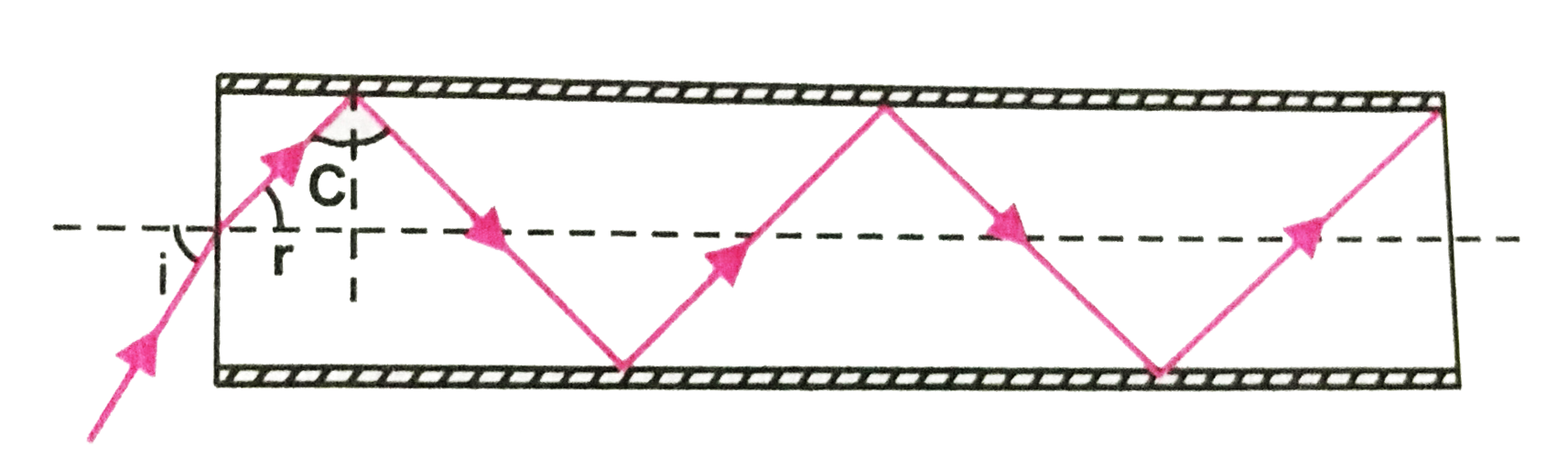
View Solutiona.Figure shows a cross-section of a 'light pipe' made of glass fibre of refractive index 1.68
The outer converting of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections insides the pipe take place as shown in the figure.
b.What is the answer if there is no outer converting of the pipe ?
View SolutionCross section of a light pipe is shown in the following figure :

Inner core is material of refractive index 1.68 and its outer covering is a material of refractive index 1.44. Find the maximum angle at which the ray can be incident with the axis of pipe for which total internal reflection occurs inside the pipe.
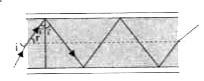
View Solution(a) Figure 9.32 shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
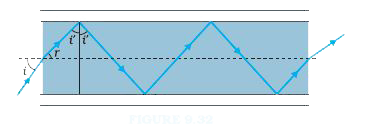
(b) What is the answer if there is no outer covering of the pipe?
View Solution
